Поперечной называют деформацию (абсолютную или относительную), которая меняет размеры сечения в направлении, перпендикулярном продольной оси бруса.
Одновременно с продольной деформацией, при действии на брус сжимающей или растягивающей силы наблюдается также поперечная деформация.
При сжатии бруса его поперечные размеры увеличиваются, а при растяжении – уменьшаются.
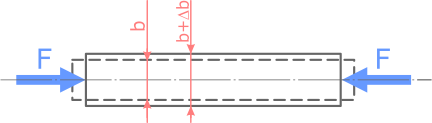
Если поперечный размер бруса до приложения к нему сжимающих сил F обозначить b, а после приложения этих сил b+Δb (рис. 1), то величина Δb будет обозначать абсолютную поперечную деформацию бруса.
Отношение Δb/b является относительной поперечной деформацией и обозначается как εпоп.
Опыт показывает, что при напряжениях, не превышающих предела упругости относительная поперечная деформация εпоп прямо пропорциональна относительной продольной деформации εпр, но имеет обратный знак:
Коэффициент пропорциональности ν зависит от материала бруса. Он называется коэффициентом поперечной деформации, или коэффициентом Пуассона, и представляет собой отношение относительной поперечной деформации к относительной продольной, взятое по абсолютной величине (модулю), т.е.
Коэффициент Пуассона ν наряду с модулем упругости Е характеризует упругие свойства материала и определяется экспериментально. Для различных материалов он изменяется от нуля (для пробкового дерева) до 0,5 (для резины, парафина).
Для металлов значения ν лежат в пределах 0,25 – 0,35.
