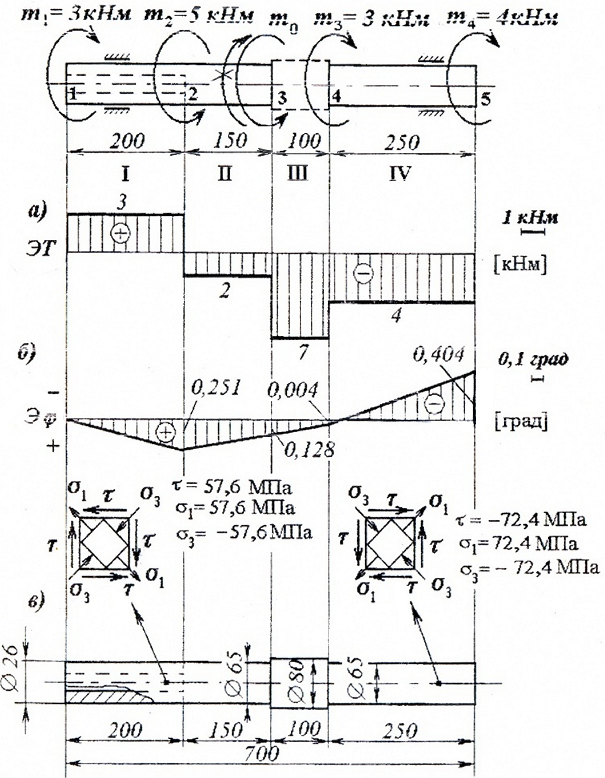
Пример решения задачи по расчёту диаметров стального ступенчатого вала сплошного и кольцевого сечения по условию прочности с построением эпюры крутящих моментов.

Задача
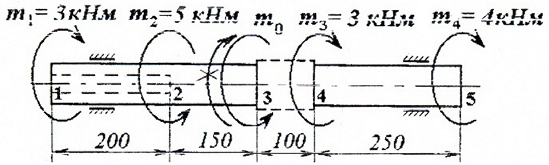
Стальной вал круглого сплошного и кольцевого сечения нагружен скручивающими моментами m₀, m₁=3кНм, m₂=5кНм, m₃=3кНм, m₄=4кНм.

Расчетная схема вала:

Другие примеры решений >
Помощь с решением задач >

Требуется спроектировать ступенчатый вал заданной формы (по конструктивным соображениям, диаметр вала на участках 1-3 и 4-5 должен быть одинаков, причем на участке 1-2 вал имеет кольцевое сечение с соотношением внутреннего и наружного диаметров: c=d/D=0,4) и построить эпюры крутящих моментов и углов закручивания сечений.

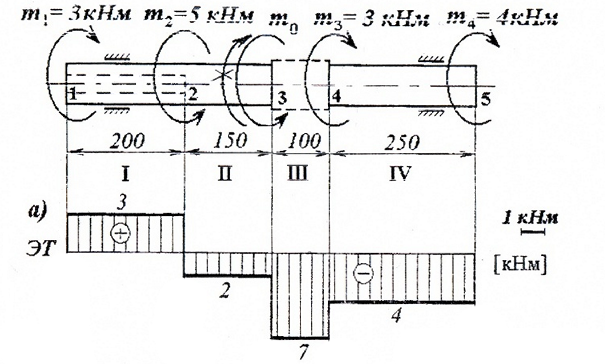
Показать напряженное состояние по участкам вала.
Принять:

• допустимые касательные напряжения [τ]=80МПа;
• модуль сдвига G=80ГПа.

Решение
Посмотреть теорию по теме «Кручение»

Определение неизвестного момента

Определим величину и направление момента m₀.
Направим m₀ произвольно, например, по ходу часовой стрелки.

Тогда из условия равновесия вала:

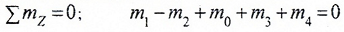
находим

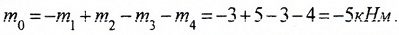
Здесь, знак “-” показывает, что направление m₀ нужно изменить на противоположное.

Расчет крутящих моментов

Величину крутящих моментов на участках вала определяем методом сечений.

С учетом правила знаков, получаем:

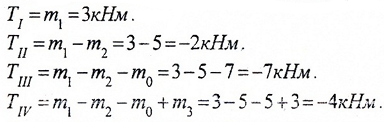
По этим значениям строим эпюру крутящих моментов T:

Расчет диаметров вала

Диаметры вала будем определять из условия прочности.
На участках I, II и IV диаметр вала одинаков.

Наружный диаметр кольцевого (полого) участка:

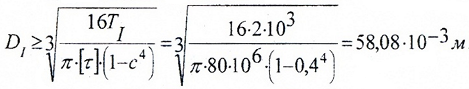
Сравнивая T_II и T_IV видим, что T_II>T_IV, поэтому:

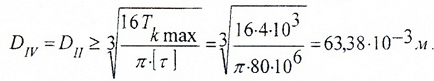
Так как 63,38>58,08 мм, выбираем большее значение.
Окончательно, согласно ГОСТ 6636, принимаем стандартное значение диаметра:

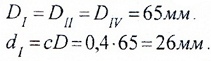
Диаметр вала на III участке (T_III=7кНм)

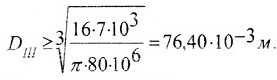
По ГОСТ, принимаем D_III=80мм.

Расчет геометрических характеристик

Вычислим геометрические характеристики сечений на участках вала.
Моменты сопротивления:

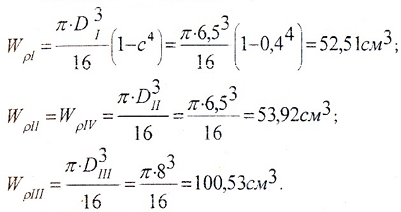
Моменты инерции

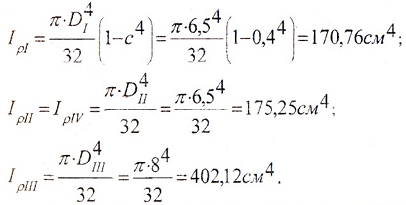
Расчет касательных напряжений

Вычисляем максимальные касательные напряжения на участках по формуле:

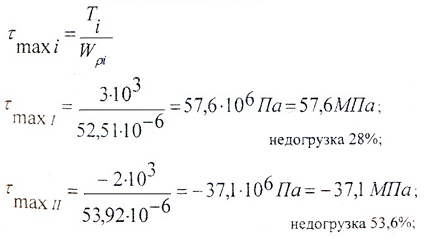
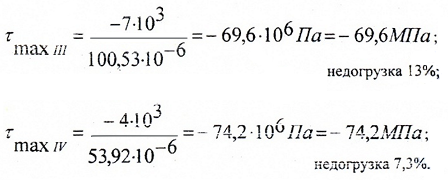
Расчет деформаций

Определяем углы закручивания участков:

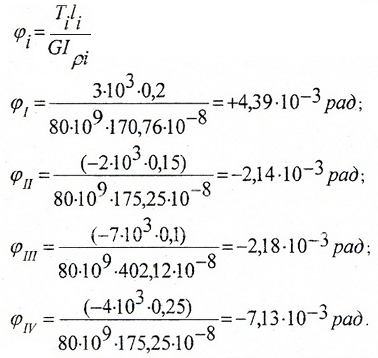
Построение эпюры перемещений

Рассчитаем углы закручивания характерных сечений.
Примем крайнее левое сечение вала за условно неподвижное.

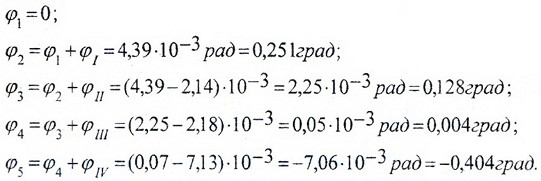
По этим значениям строим эпюру углов закручивания сечений и вычерчиваем эскиз спроектированного вала.

Другие примеры решения задач >
Лекции по сопромату >