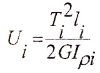Кручением называется такой вид деформации бруса, при котором в его поперечных сечениях возникает только один внутренний силовой фактор – крутящий момент T.

Брусья, испытывающие кручение, принято называть валами.

Внутренний крутящий момент

Внутренние скручивающие моменты появляются под действием внешних крутящих моментов m_i, расположенных в плоскостях, перпендикулярных к продольной оси бруса.

Скручивающие моменты передаются на вал в местах посадки зубчатых колес, шкивов ременных передач и т.п.

Величина крутящего момента в любом сечении вала определяется методом сечений:

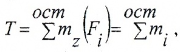
т.е. крутящий момент численно равен алгебраической сумме скручивающих моментов m_i, расположенных по одну сторону от рассматриваемого сечения.

Правило знаков внутренних скручивающих моментов:
Положительными принимаются внутренние моменты, стремящиеся повернуть рассматриваемую часть вала против хода часовой стрелки, при рассмотрении со стороны отброшенной части вала.

В технике наиболее широко используются валы круглого поперечного сечения.

Теория кручения круглых валов основана на следующих гипотезах:

1. поперечное сечение, плоское до деформации вала, остается плоским и после деформации;
2. радиусы, проведенные мысленно в любом поперечном сечении, в процессе деформации вала не искривляются.

Напряжения при кручении

В поперечных сечениях вала при кручении имеют место только касательные напряжения.
Касательные напряжения, направленные перпендикулярно к радиусам, для произвольной точки, отстоящей на расстоянии ρ от центра, вычисляются по формуле:

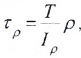
где I_ρ — полярный момент инерции.
Эпюра касательных напряжений при кручении имеет следующий вид:

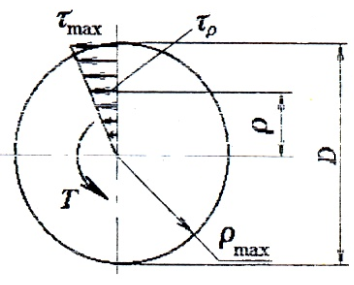
Касательные напряжения меняются по линейному закону и достигают максимального значения на контуре сечения при ρ= ρ_max:

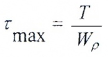
Здесь:

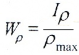
— полярный момент сопротивления.
Геометрические характеристики сечений:
а) для полого вала:


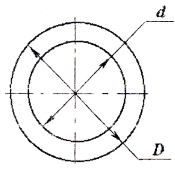
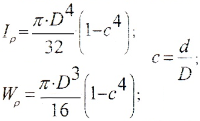
б) для вала сплошного сечения (c=0)

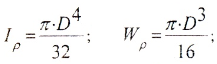
в) для тонкостенной трубы (t<0,9)

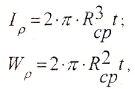
где

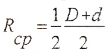
— радиус срединной поверхности трубы.

Деформации

Деформации валов при кручении заключаются в повороте одного сечения относительно другого.

Угол закручивания вала на длине Z определяется по формуле:

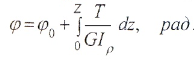
Если крутящий момент и величина GI_ρ, называемая жесткостью поперечного сечения при кручении, постоянны, для участка вала длиной l имеем:

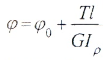
Угол закручивания, приходящийся на единицу длины, называют относительным углом закручивания:

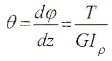
Расчет валов сводится к одновременному выполнению двух условий:

1. условию прочности:
   
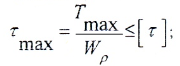
2. условию жесткости:
   

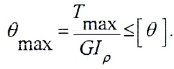
Для стальных валов принимается:

• допускаемое касательное напряжение
  
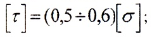
• допускаемый относительный угол закручивания
  

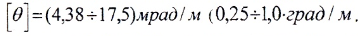
Используя условия прочности и жесткости, как и при растяжении – сжатии можно решать три типа задач:

1. проверочный расчет, заключающийся в проверке выполнения условий прочности и жесткости при известных значениях крутящего момента, размеров и материала вала.
2. Проектировочный расчет, при котором вычисляются диаметры:
   
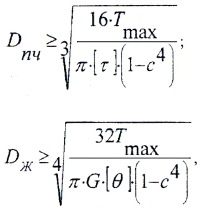
   при этом берется большее из найденных значений, а затем принимается стандартное значение по ГОСТ.
3. Определение грузоподъемности вала:
   • из условия прочности
     
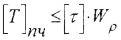
   • из условия жесткости
     

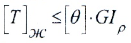
   Из двух найденных значений крутящего момента необходимо принять меньшее.

При кручении, наряду с касательными напряжениями в поперечных сечениях, в соответствии с законом парности, касательные напряжения возникают и в продольных сечениях. Таким образом, во всех точках вала имеет место чистый сдвиг.

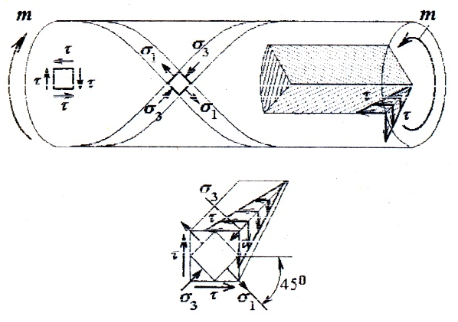
Главные напряжения σ₁ = τ, σ₃ = -τ наклонены под углом α=±45^о к образующей.

Потенциальная энергия упругой деформации определяется по формуле

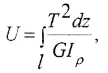
или для участка вала при постоянном T и GI_ρ

---

Далее: