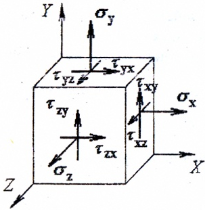
Теория напряженного состояния в окрестности точки деформируемого тела рассматривает совокупность напряжений, действующих по площадкам, проведенным через исследуемую точку.
На площадках общего положения действуют нормальные и касательные напряжения (рис. 1).
Правило знаков для этих напряжений в сопротивлении материалов принимается следующим: положительные нормальные напряжения направлены от сечения, а положительные касательные напряжения стремятся повернуть элемент по направлению хода часовой стрелки.
Площадки, на которых отсутствуют касательные напряжения, называются главными площадками, а нормальные напряжения, действующие по этим площадкам, — главными напряжениями.
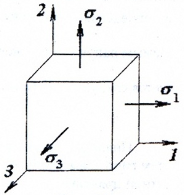
В любой точке деформируемого тела можно выделить три взаимно перпендикулярные главные площадки, по которым действуют главные напряжения σ1, σ2 и σ3, причем σ1 ≥ σ2 ≥ σ3.
Если два главных напряжения из трех равны нулю, то такое напряженное состояние называется линейным или одноосным. Оно соответствует центральному (осевому) растяжению или сжатию и рассмотрено в предыдущем разделе.
Если одно из трех главных напряжений равно нулю, то такое напряженное состояние называется плоским или двуосным. Пример плоского напряженного состояния показан на рис. 2.
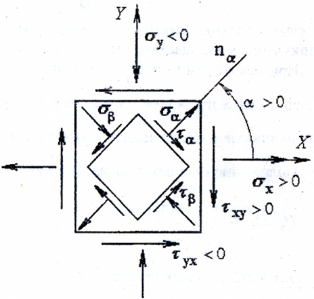
Одноименные напряжения на параллельных гранях бесконечно малого элемента численно равны друг другу. При плоском напряженном состоянии две противоположные грани всегда свободны от напряжений (на рис. 2 это фасадная и тыльная грани).
По закону парности касательных напряжений касательные напряжения на взаимно перпендикулярных площадках равны по величине и противоположны по знаку, т.е.
τxy=-τyx.
При повороте прямоугольного элемента на угол α напряжения на его гранях изменяются и вычисляются по формулам:
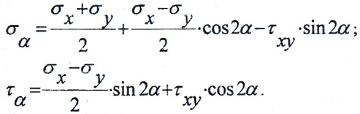
По закону парности касательных напряжений τα= -τβ.
Величины σ связаны законом суммы нормальных напряжений
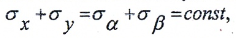
т.е. сумма величин нормальных напряжений, действующих по взаимно перпендикулярным площадкам, есть величина постоянная.
При некотором угле α0 касательные напряжения равны нулю, нормальные напряжения по данной площадке в данной точке максимальны (σmax), а на перпендикулярной площадке – минимальны (σmin).
Положение главных площадок определяется по формуле
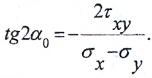
Значения главных напряжений вычисляются по выражению
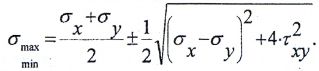
Наибольшие касательные напряжения действуют на площадках, наклонных к главным под углом 450 и рассчитываются по формулам:
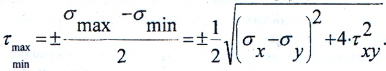
Нормальные напряжения на этих площадках можно найти по формуле
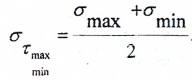
Относительные линейные и угловые деформации ребер элемента можно вычислить на основании обобщенного закона Гука. Для плоского напряженного состояния
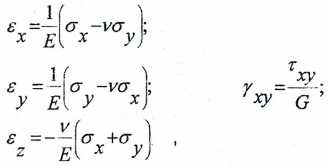
где
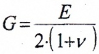
— модуль сдвига материала. Для стали G=80ГПа.
Относительное изменение объема материала в окрестностях исследуемой точки определяется по формуле
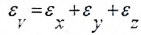
Удельная потенциальная энергия для плоского напряженного состояния
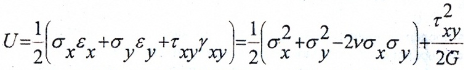
Напряженное состояние называется объемным или трехосным (рис. 3), если
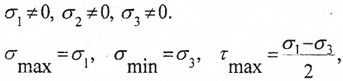
Относительное изменение объема
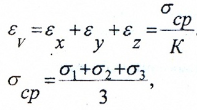
где K – модуль объемной деформации
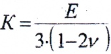
Удельная потенциальная энергия упругой деформации:
— полная
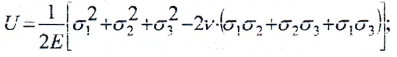
— изменения объема
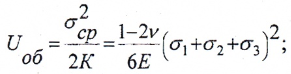
— изменения формы
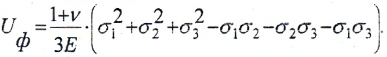
Относительные деформации и напряжения связаны обобщенным законом Гука:
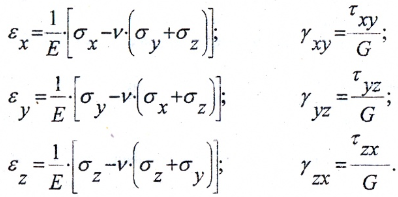
Теории прочности
Для проверки прочности материала при плоском и объемном напряженном состояниях используются гипотезы (теории) прочности.
Каждая гипотеза прочности высказывает свое предположение о том, какой фактор вызывает появление опасного (предельного) состояния.
В зависимости от принятой гипотезы определяют эквивалентное напряжение σэкв и сравнивают его с допустимым напряжением на растяжение [σ], то есть условие прочности записывается следующим образом:
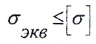
Приведем зависимости для вычисления эквивалентных напряжений по трем гипотезам прочности, наиболее широко применяемым в современной расчетной практике.
Гипотеза наибольших касательных напряжений (III теория прочности)
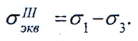
Четвертая (энергетическая) гипотеза прочности
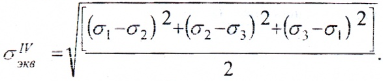
Гипотеза прочности Мора
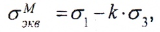
где коэффициент k представляет собой отношение предельных напряжений при одноосном растяжении и сжатии. Можно принять
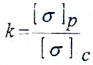
III и IV гипотезы применяют для оценки прочности пластичных материалов, а гипотезу Мора – как для пластичных, так и для хрупких.
