Принцип Даламбера для материальной точки гласит: для движущейся точки в любой момент времени геометрическая сумма действующих на точку активных сил, реакций связи и сил инерции равна нулю.
Другими словами, все внешние силы действующие на материальную точку при её движении всегда уравновешиваются силами инерции.
Многообразие решаемых в механике задач требует разработки различных методов составления уравнений движения механических систем. Одним из таких методов, позволяющих с помощью уравнений описать движение произвольной системы, является принцип Даламбера.
Для несвободной материальной точки на основании второго закона динамики запишем:
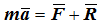
где R — реакция связи.
Приняв
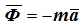
гдe Ф — сила инерции, получим
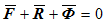
Эта формула выражает принцип Даламбера для материальной точки.
Этот принцип позволяет писать уравнения статики для движущейся точки.
Примеры решения задач >
Принцип Даламбера для механической системы >
