Пример решения задачи по определению закона относительного движения точки, которая движется вдоль тела, вращающегося вокруг вертикальной оси с постоянной угловой скоростью.
Задача
Тело D вращается вокруг вертикальной оси с постоянной угловой скоростью ω. По цилиндрическому каналу движется шарик M (рисунок 8).
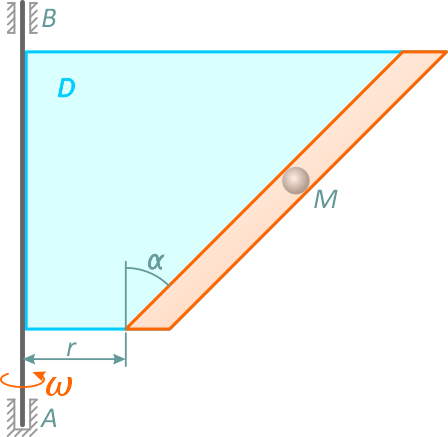
Определить закон относительного движения точки M как точки x = x(t). Найти также координату x и давление шарика на стенку канала в момент времени t = τ, если α = 45°, ω = 10 с-1; m = 0,01 кг; τ = 0,2 c; x0 = 0; V0 отн= 0; r = 0,2 м.
Другие примеры решений >
Помощь с решением задач >
Решение
Свяжем подвижную систему отсчета Oxyz с вращающимся каналом, совместив ось x с траекторией относительного движения точки M.
Вращение этой системы относительно оси АВ является переносным движением для точки M. Движение точки вдоль канала будет относительным.
К шарику приложены: вес G и нормальная реакция стенки канала, которую разложим на две составляющие N1 и N2. Присоединим к силам, действующим на шарик, кориолисову силу инерции Фкор и переносную силу инерции Фnпер.
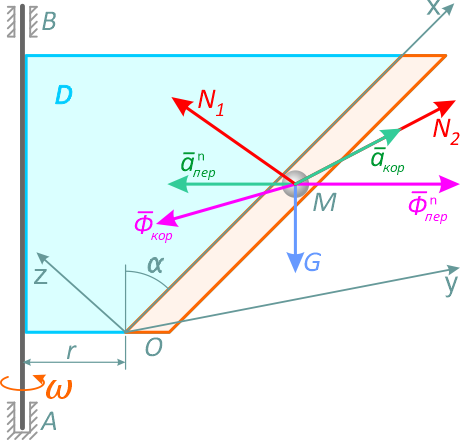
Поскольку вращение происходит с постоянной угловой скоростью, переносное ускорение точки M имеет только нормальную составляющую. Соответственно переносная сила инерции будет иметь одну составляющую, направленную от оси AB.
В литературе ее называют центробежной силой инерции. Направление ускорения Кориолиса найдем по правилу Жуковского (рисунок 8.1), полагая, что шарик движется от точки O.
Модули сил инерции определяются по формулам
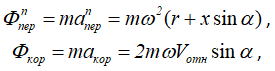
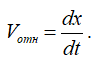
Основное уравнение относительного движения, в данном случае, имеет вид
![]()
Проецируя это уравнение на подвижные оси координат, получим
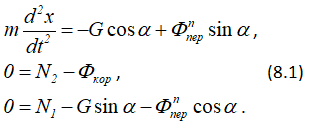
Подставляя значение Фnпер в первое уравнение системы (8.1), получим
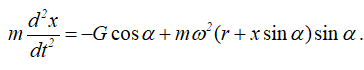
Последнее уравнение представим в виде
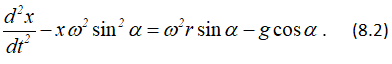
Это линейное неоднородное дифференциальное уравнение второго порядка. Общее решение полученного уравнения имеет вид
где x* – общее решение однородного уравнения
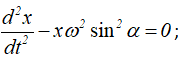
x** – частное решение уравнения (8.2).
Составим характеристическое уравнение и найдем его корни
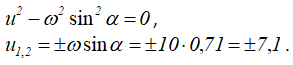
Таким образом, общее решение однородного уравнения
![]()
Частное решение уравнения (8.2) находим в виде
Подставляя в (8.2), получаем
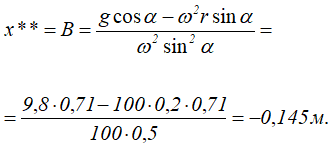
Общее решение дифференциального уравнения (8.2) получает вид
![]()
![]()
Постоянные C1 и C2 определяем из начальных условий:
![]()
Тогда при t = 0 получим
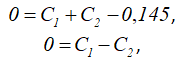
отсюда C1=C2=0,0725 м.
Уравнение относительного движения принимает вид
![]()
Скорость относительного движения
![]()
Из второго и третьего уравнений системы (8.1) определим реакцию стенок канала в момент времени t=0,2 с
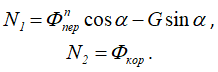
Из этих уравнений найдем
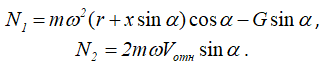
Для определения числовых значений реакции необходимо найти значения координаты x и относительной скорости при t=0,2 с.
Подставляя t=0,2 с в (8.3) и (8.4), получим
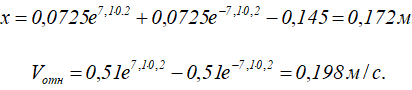
Следовательно, составляющие реакции N1 и N2 будут равны
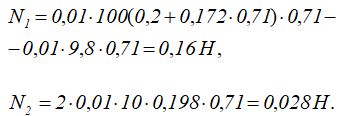
Реакция стенки канала
![]()
