Теорема об изменении момента количества движения (кинетического момента) материальной точки:
Рассмотрим материальную точку M массой m, движущуюся под действием силы F (рисунок 3.1). Запишем и построим вектор момента количества движения (кинетического момента) M0 материальной точки относительно центра O:
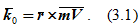
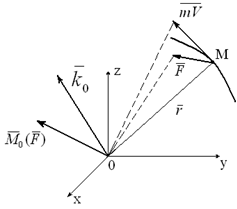
Дифференцируем выражение момента количества движения (кинетического момента k0) по времени:
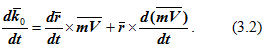
Так как dr/dt=V, то векторное произведение V × m∙V (коллинеарных векторов V и m∙V) равно нулю. В то же время d(m∙V)/dt=F согласно теореме о количестве движения материальной точки. Поэтому получаем, что
где r×F = M0 (F) – вектор-момент силы F относительно неподвижного центра O. Вектор k0 ⊥ плоскости (r, m×V), а вектор M0(F) ⊥ плоскости (r, F), окончательно имеем
Уравнение (3.4) выражает теорему об изменении момента количества движения (кинетического момента) материальной точки относительно центра, которая гласит: производная по времени от момента количества движения (кинетического момента) материальной точки относительно какого-либо неподвижного центра равна моменту действующей на точку силы относительно того же центра.
Проецируя равенство (3.4) на оси декартовых координат, получаем
dkx/dt = Mx(F);dky/dt = My(F);dkz/dt = Mz(F). (3.5)
Равенства (3.5) выражают теорему об изменении момента количества движения (кинетического момента) материальной точки относительно оси: производная по времени от момента количества движения (кинетического момента) материальной точки относительно какой-либо неподвижной оси равна моменту действующей на эту точку силы относительно той же оси.
Рассмотрим следствия, вытекающие из теорем (3.4) и (3.5).
Следствие 1
Рассмотрим случай, когда сила F во все время движения точки проходит через неподвижный центр O (случай центральной силы), т.е. когда M0(F) = 0. Тогда из теоремы (3.4) следует, что k0 = const, т.е. в случае центральной силы момент количества движения (кинетический момент) материальной точки относительно центра этой силы остается постоянным по модулю и направлению (рисунок 3.2).
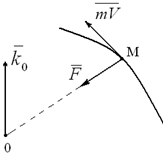
Из условия k0 = const следует, что траектория движущейся точки представляет собой плоскую кривую, плоскость которой проходит через центр этой силы.
Следствие 2
Пусть Mz(F) = 0, т.е. сила пересекает ось z или параллельна ей.
В этом случае, как это видно из третьего из уравнений (3.5), kz = const, т.е. если момент действующей на точку силы относительно какой-либо неподвижной оси всегда равен нулю, то момент количества движения (кинетический момент) точки относительно этой оси остается постоянным.
Далее: