Внецентренным нагружением называют случай, когда продольная сжимающая либо растягивающая сила приложена не к центру тяжести сечения, а с некоторым смещением от него, называемым эксцентриситетом (рис. 7.2).
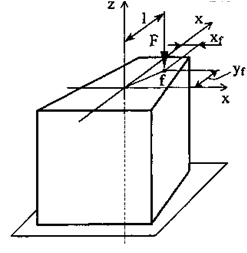
Рис. 7.2
Распределение нормальных напряжений (рис. 7.3):
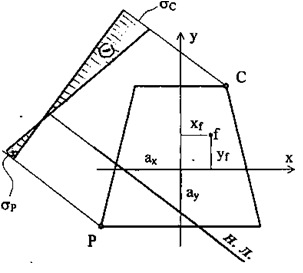
Рис. 7.3
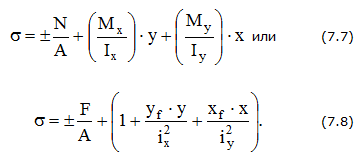
Знак «+» соответствует растяжению, а знак «-» – сжатию.
Отрезки, отсекаемые нейтральной линией на осях координат
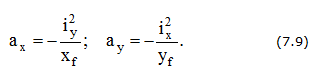
Условие прочности
Условия прочности при внецентренном сжатии
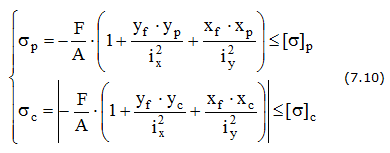
Ядро сечения
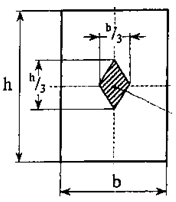
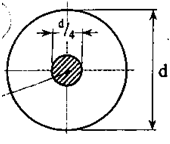
Рис. 7.4
Координаты вершин ядра сечения (рис. 7.4):
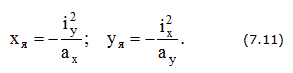
Далее: