При растяжении-сжатии, по условию жесткости, деформации не должны превышать допустимых значений.
В противном случае, жесткость бруса не обеспечена
Деформации
При осевом растяжении и сжатии наблюдаются абсолютные и относительные деформации (рис. 4.1,а):
l1 – l = Δl — абсолютная продольная деформация (удлинение);
h1 – h = -Δh — абсолютная поперечная деформация (сужение);
относительная продольная деформация:
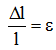
относительная поперечная деформация:
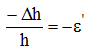
Отношение
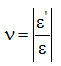
называется коэффициентом поперечной деформации (коэффициентом Пуассона).
Напряжения и деформации взаимосвязаны законом Гука
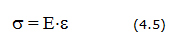
где Е — модуль упругости (модуль Юнга).
В общем случае удлинение стержня определяется по формуле
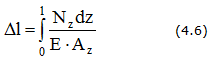
В частном случае, когда жесткость сечения ЕА = const и NZ= F = const
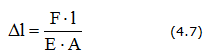
При ступенчатом изменении нагрузки Nz и конфигурации сечения
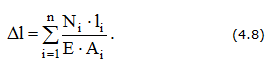
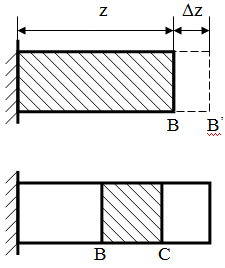
В результате деформации бруса его поперечные сечения получают линейные перемещения U(z). Так, перемещение сечения В, находящегося на расстоянии z от закрепленного конца, равно удлинению Δlz части бруса длиной z, заключенной между неподвижным и рассматриваемым сечением.
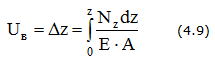
Взаимное перемещение двух сечений В и С бруса равно удлинению части бруса, заключенной между этими сечениями
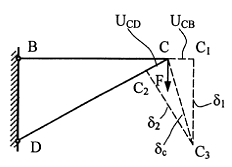
Перемещение точек стержневой системы (BCD) (Рис. 4.3) происходит как за счет продольных деформаций (UСВ = ΔlBC, UCD = ΔlDC), так и за счет поворота деформированных стержней BC1 и DC2 относительно шарниров (B, D) как твердого тела по дугам С1С3 = δ1 и С2С3 = δ2, замененными перпендикулярами к радиусам поворота (ВС1 и DС2).
Отрезок СС3 = δс соответствует полному перемещению узла С в результате деформации стержней ВС и DС.
Условие жесткости
Условие жесткости стержня
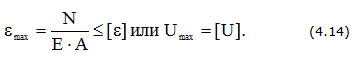
Условие жесткости узла стержневой системы

Потенциальная энергия упругой деформации стержня
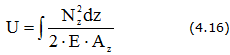
Далее: