Растяжением и сжатием называют такой вид деформации бруса, при котором в его поперечных сечениях возникает единственный внутренний силовой фактор – продольная сила N.
Брус при растяжении-сжатии называют стержнем.
Для определения продольной силы используется метод сечений:
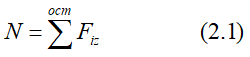
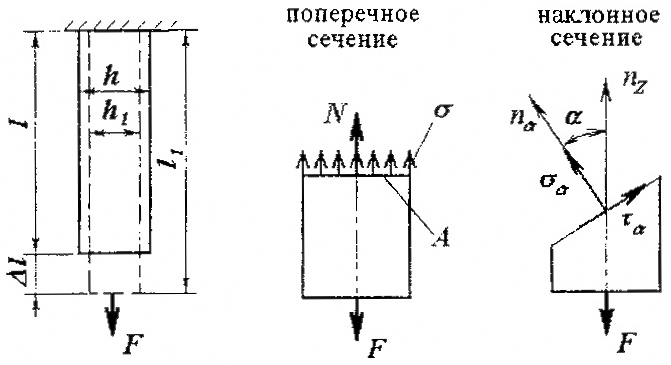
В сечениях бруса, удаленных более чем на величину h (рис. 2.1) от торцов (мест нагружения), усилие N на основании принципа Сен-Венана равномерно распределяется по площади поперечного сечения, вызывая нормальные напряжения:

В наклонном сечении возникают нормальные σα и касательные τα напряжения:
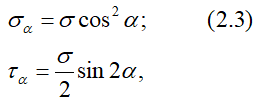
причем
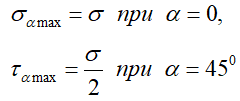
При растяжении (сжатии) имеют место только линейные деформации:
— абсолютная продольная деформация (удлинение/укорочение)
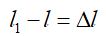
— абсолютная продольная деформация (сужение/утолщение)
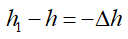
— относительная продольная деформация
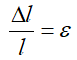
— относительная поперечная деформация
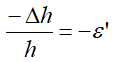
Отношение

называется коэффициентом поперечной деформации (коэффициентом Пуассона).
Напряжения и деформации взаимосвязаны законом Гука

где:
E – модуль упругости I рода (модуль Юнга), является постоянной величиной для данного материала и характеризует его жесткость, для стали E=200ГПа.
Изменение длины участка бруса постоянного сечения вычисляется по формуле
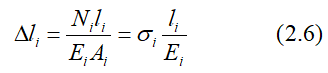
Величина EiAi называется жесткостью поперечного сечения бруса при растяжении (сжатии).
Полное удлинение (укорочение) бруса с несколькими силовыми участками:
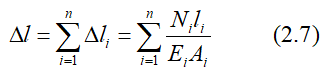
Условие прочности при растяжении/сжатии выражается неравенством:
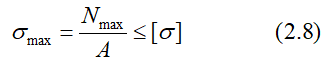
Здесь
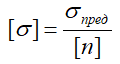
— допускаемое напряжение;
σпред — предельное (опасное) для данного материала напряжение, равное пределу текучести (σТ или σ0,2) для пластичных материалов или пределу прочности σпч для хрупких материалов;
[n] – нормативный коэффициент запаса прочности.
Условие прочности позволяет решать три типа задач:
1. Проверка прочности (проверочный расчет)
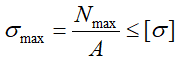
2. Подбор сечения (проектировочный расчет)
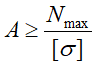
3. Определение грузоподъемности (допускаемой нагрузки)
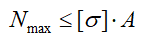
При расчете на жесткость растянутого (сжатого) бруса обычно определяют величину продольной деформации, которая не должна превышать допустимых значений, т.е.

Далее: