Решение задачи по определению аналитическим и графическим способами реакций связей в шарнирном соединении невесомой стержневой системы, нагруженной двумя силами, лежащими в одной плоскости.

Задача

Определить реакции связей системы стержней, удерживающих подвешенные на нерастяжимых нитях грузы 1 и 2.

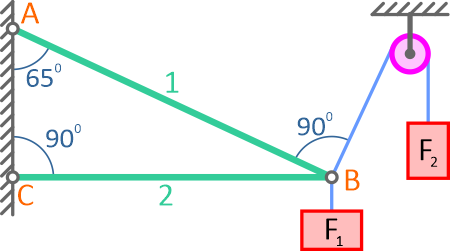
Масса грузов: F₁ = 0,4кН и F₂ = 0,5кН (рис. 1). Весом стержней пренебречь.
Найденные аналитическим способом значения требуется проверить графически.

Решение

1. Рассматриваем равновесие шарнира В.
2. Освобождаем шарнир В от связей и изображаем действующие на него активные силы и реакции связей, располагая их вдоль оси стержней (рис. 2).

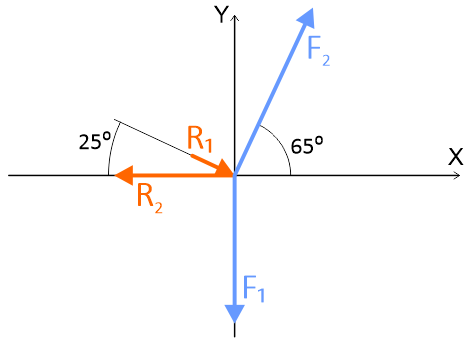
Аналитический способ решения задачи

Аналитическим называют способ решения, при котором искомые результаты получают путем расчетов по составленным выражениям.

Другие видео

Выбираем систему координат и составляем уравнения равновесия для системы сил, действующих на шарнир В.

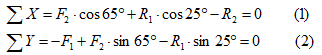
Определяем реакции стержней R₁ и R₂, решая уравнения (1) и (2).
Из уравнения (1) получаем:

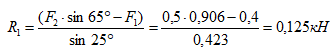
Подставляем найденное значение R₁ в уравнение (2) и получаем

Положительные значения реакций связей R₁ и R₂ указывают на то, что первоначально выбранные направления реакций оказались верными.

Графическое решение. Силовой многоугольник

Проверяем правильность полученных результатов, решая задачу графически.

Полученная система сил находится в равновесии, следовательно, силовой многоугольник, построенный для этой системы сил, должен быть замкнутым.

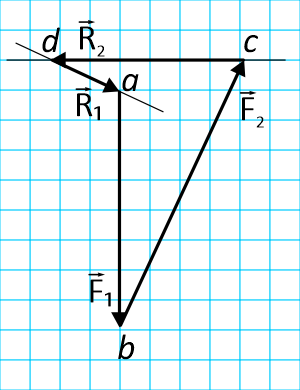
Строим силовой многоугольник (рис. 3) в следующем порядке:

1. В выбранном масштабе (например: μ_сил=0,01кН/мм) из точки a откладываем, путем параллельного переноса, заданную силу F₁
2. От конца вектора F₁ (точки b) под заданным углом откладываем силу F₂
3. Из точек а и с проводим прямые, параллельные положениям стержней 1 и 2.
   Эти прямые пересекаются в точке d и в результате построения образуется замкнутый многоугольник abcd, в котором сторона cd=R₂, а сторона da=R₁.

Измерив длины этих сторон линейкой (в мм) и умножив на масштаб μ_сил построения сил, получаем значения искомых реакций связей в стержнях:

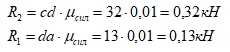
Как видно из чертежа, графическое решение задачи подтверждает правильность аналитического решения.

Другие примеры решения задач статики >