Равновесием произвольной плоской системы сил называют её состояние, при котором система неподвижна (статична), т.е. когда она не движется вдоль координатных осей и не вращается в их плоскости.
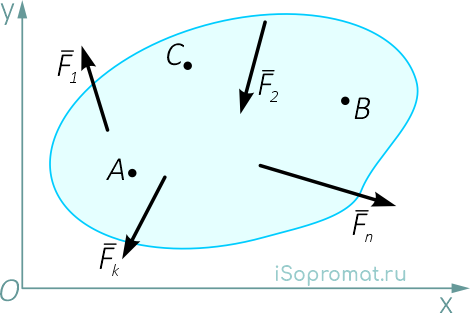
Для равновесия произвольной плоской системы сил, приложенных к твёрдому телу и не пересекающихся в одной точке, необходимо и достаточно, чтобы главный вектор R этих сил и их главный момент MO относительно произвольной точки O, лежащей в плоскости действия этих сил, были равны нулю, т.е.
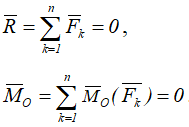
В координатной форме эти условия выражаются следующими тремя уравнениями:
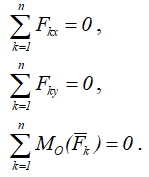
причем направление осей и положение точки O, относительно которой составляются уравнения моментов, можно выбирать произвольно.
Эти уравнения имеют вид первой формы равновесия для произвольной плоской системы сил.
Условия равновесия плоской системы сил, расположенных произвольно на плоскости, можно выразить ещё в двух других видах:
Вторая форма равновесия (теорема о трёх моментах) – алгебраические суммы моментов сил относительно трёх произвольных точек A, B и C, не лежащих на одной прямой, равны нулю, т.е.
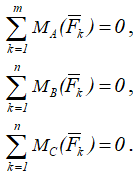
Третья форма равновесия – алгебраические суммы моментов всех сил относительно двух любых точек A и B равны нулю и сумма проекций этих сил на ось Ox, не перпендикулярную к прямой, проходящей через точки A и B, равна нулю, т.е.
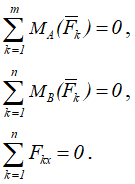
Частные случаи равновесия
В частном случае, если линии действия всех сил плоской системы параллельны (плоская система параллельных сил),
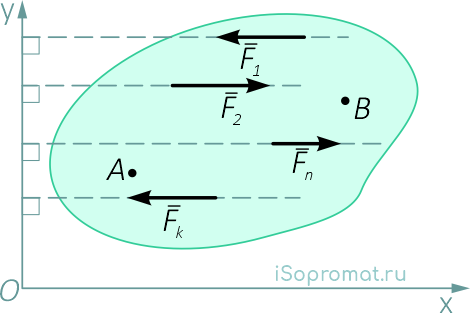
то условия равновесия таких сил можно выразить не тремя, а двумя уравнениями:
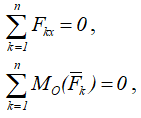
В этом случае ось Ox можно направить параллельно данным силам, или
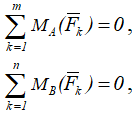
если прямая AB не параллельна данным силам.
Для исследования равновесия плоской системы сходящихся сил
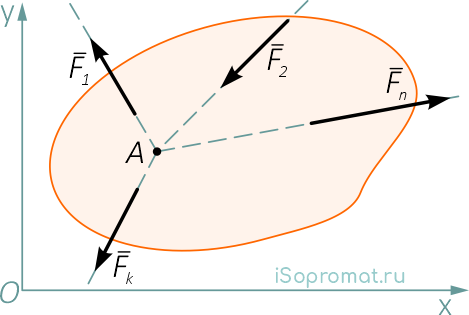
тоже достаточно двух уравнений
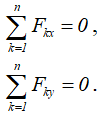
В задачах такого типа число неизвестных плоской системы сил не должно превышать трех, иначе система станет статически неопределимой.
Далее: