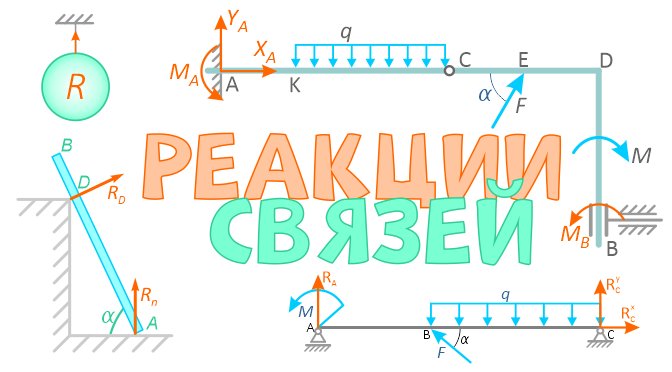
Связями называют тела, ограничивающие свободу перемещения рассматриваемого тела.

Реакции связей — это усилия, с которыми связи действуют на данное тело, удерживая его в состоянии статического равновесия.

Тела в природе бывают свободными и несвободными. Тела, свобода перемещения которых ничем не ограничена, называются свободными.

Одним из основных положений механики является принцип освобождаемости от связей, согласно которому несвободное тело можно рассматривать как свободное, если отбросить действующие на него связи и заменить их силами – реакциями связей.

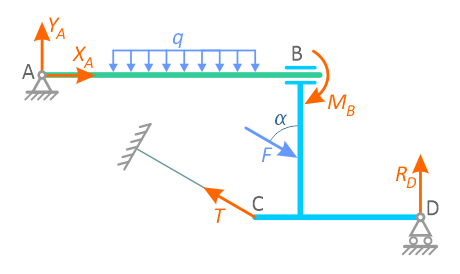
Очень важно правильно расставить реакции связей, иначе составленные уравнения равновесия окажутся неверными.

Рассмотрим реакции связей основных типов, встречающихся при решении задач: гладкой поверхности, ребра, гибкой нити, стержня, шарнирных опор и заделок, а также примеры замены связей их реакциями.

Реакции гладкой поверхности и ребра

Ниже приведены примеры замены связей гладкой поверхности и ребра их реакциями.

На рисунках 1.1–1.8 показаны примеры замены реакциями сил, расположенных в плоскости.

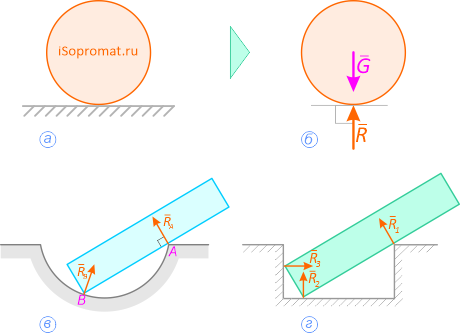
а – тело весом G на гладкой поверхности;
б – действие поверхности заменено реакцией – силой R;
в – в точке А связь «опорная точка» или ребро;
г – реакции направлены перпендикулярно опираемой или опирающейся плоскостям

Реакция гладкой поверхности всегда направлена по нормали к этой поверхности (рисунок 1.1).

Реакции связей нити и стержня

Реакция «невесомого» троса (нити, цепи, стержня) всегда направлена вдоль самого троса (нити, цепи, стержня) (рисунок 1.2).

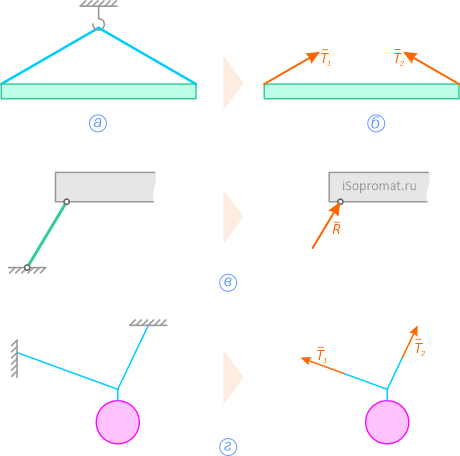
а – балка висит на двух тросах;
б – действие тросов заменено силами Т₁ и Т₂;
в – связь «идеальный стержень»;
г – связи «идеальная нить»

Реакции связей шарнирных опор

Шарнирные опоры допускают вращение относительно шарнира, поэтому в них не возникает вращающий момент.

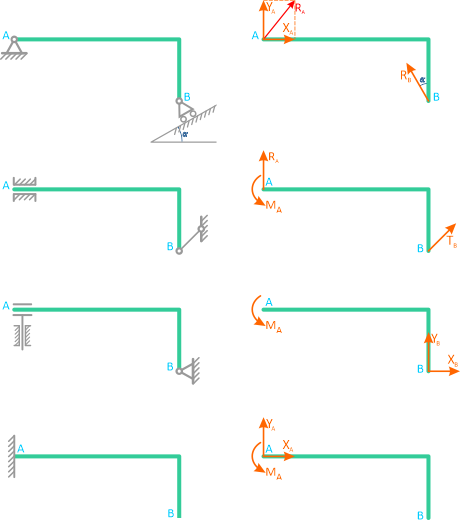
Шарнирно-неподвижная опора может изображаться по-разному (рисунок 1.3,а или 1.3,б). Она может быть заменена либо силой R с углом α (рисунок 1.3,в), либо двумя силами, например, X_A и Y_A (рисунок 1.3,г).

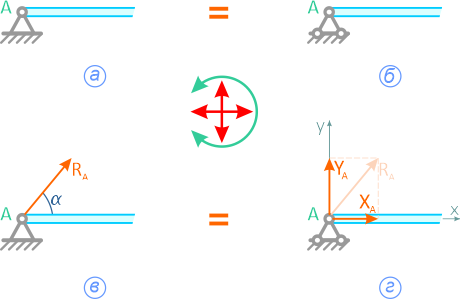
Всегда можно перейти от R и α к X_A и Y_A (и наоборот):

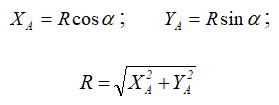
Шарнирно-подвижная опора (рисунок 1.4,а, б, в) допускает (в данном случае) горизонтальное перемещение и не допускает вертикальное.

Реакция R может быть направлена только по нормали к опорной поверхности (рисунок 1.4, г).

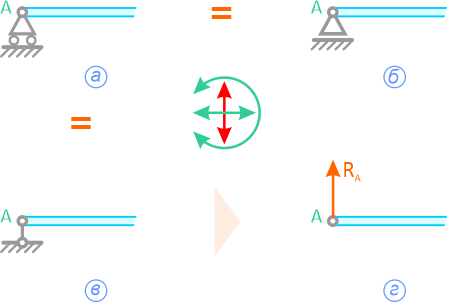
В следующем примере, связи шарнирно-неподвижной опоры в точке A и шарнирно-подвижной опоры в точке B отброшены (рисунок 1.5, б), а их действие заменено силами X_A, Y_A и R_B.

Подробнее про связи и реакции связей смотрите в нашем видео:

Другие видео

Реакции связи в заделках

Все виды заделок исключают поворот заделанных элементов, поэтому в них всегда возникает связь «момент».

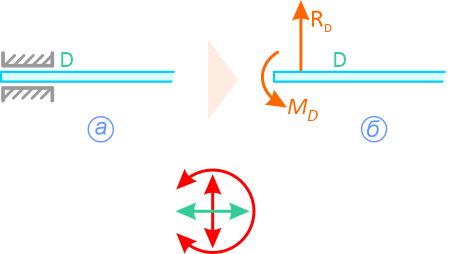
Соединение стержня и втулки в плоскости (рисунок 1.6) – скользящая заделка. Отбросив втулку – получаем действие на стержень силы R_D и момента M_D.

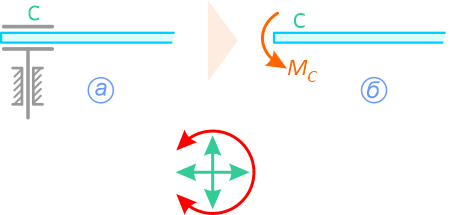
На рисунке 1.7, а изображена бискользящая заделка. В плоскости данная опора допускает поступательное перемещение стержня, как по горизонтали, так и по вертикали, но препятствует повороту (в плоскости). Реакцией такой опоры будет только момент M_C (рисунок 1.7, б).

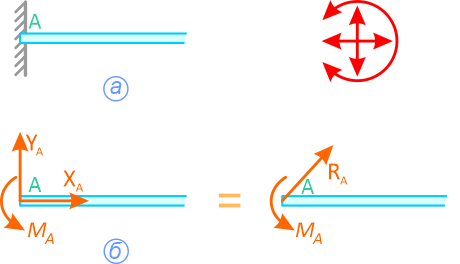
Консоль (глухая или жесткая заделка) не допускает никакого перемещения детали. Реакцией такой опоры являются неизвестная по величине и направлению сила R_A с углом α (или X_A и Y_A) и момент Μ_A (рисунок 1.8).

Реакции пространственных связей

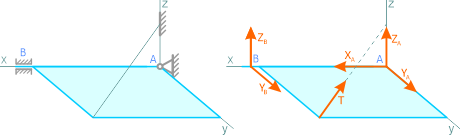
Трехмерная шарнирно-неподвижная опора, или сферический шарнир (рисунок 1.9, а), заменяется системой сил (рисунок 1.9, б) X_A, Y_A и Z_A, т.е. силой, неизвестной по величине и направлению.

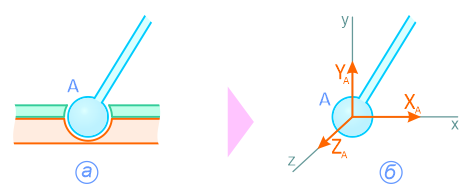
На рисунке 1.10, а показан вал с колесом, закрепленный в опорах: в точке A – подпятник или стакан, в точке B – втулка или подшипник. Действие опор заменено силами X_A, Y_A, Z_A и X_B, Z_B (рисунок 1.10, б).

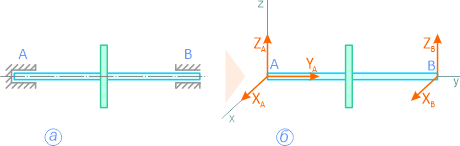
На следующих рисунках показаны примеры замены различных типов связей их реакциями.

Трехмерная система, удерживаемая в равновесии тремя типами связей: скользящей заделкой, шарнирно неподвижной опорой и тросом.

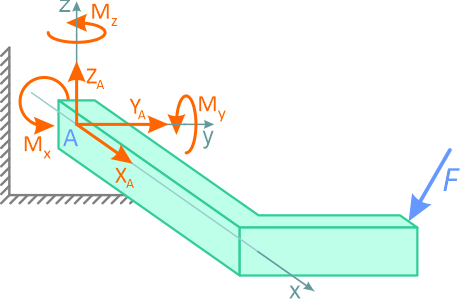
В общем случае пространственного нагружения, в глухой заделке может возникать до шести реакций связей: три силы и три момента.

Величина и истинное направление сил реакций связей определяются из уравнений равновесия рассматриваемой системы.

Для плоской системы сил можно составить 3 уравнения

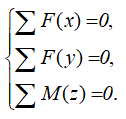
Для пространственной системы — до шести уравнений статики

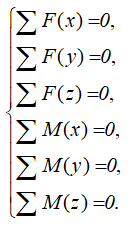
из которых выражаются и рассчитываются искомые реакции.

Пример определения направления и величины сил реакций связей

Задача

Жесткая рама закреплена в точке A шарнирной связью, а в точке B удерживается в состоянии статического равновесия опорой на катках, с упором в наклонную плоскость под углом 30°.

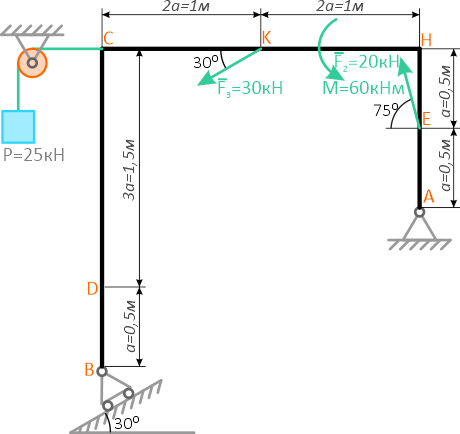
В точке C к раме привязан трос, перекинутый через блок и несущий на конце груз весом P=25кН.

На раму действует пара сил с моментом M=60кНм и две силы F₂ и F₃ приложенные в точках K и E и расположенные под углами 30° и 75° к горизонтальной оси.

Требуется определить реакции связей в точках A и B, вызываемые заданными действующими нагрузками.

При расчетах, принять размер a=0,5м.

Пример решения

Рассмотрим равновесие рамной пластины.

Проведем координатные оси x-y и изобразим действующие на пластину внешние нагрузки: силы F, пару сил с моментом M, натяжение троса T (по модулю T=P) и реакции связей X_A, Y_A, R_B.

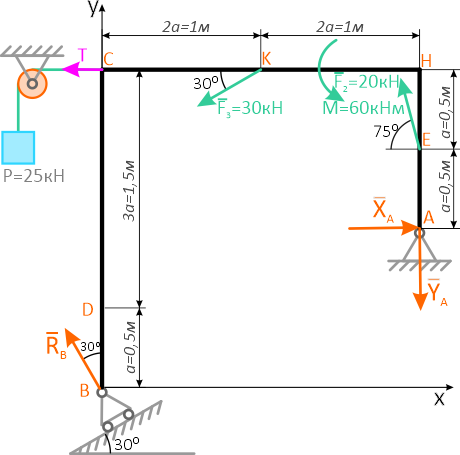
Реакцию неподвижной шарнирной опоры A изображаем двумя составляющими её связями. Реакция на катке направлена перпендикулярно опорной плоскости.

Для полученной плоской системы сил составим три уравнения равновесия системы.

При вычислении моментов сил F относительно точки A воспользуемся теоремой Вариньона, т.е. разложим силы на составляющие F_x=Fcosα и F_y=Fsinα и учтём что момент силы относительно точки равен сумме моментов составляющих этой силы относительно этой же точки, т.е. m_A(F)=m_A(F_x)+m_A(F_y).

Запишем уравнения сумм проекций сил на оси x и y, а также суммы моментов относительно любой точки системы, например, точки A.

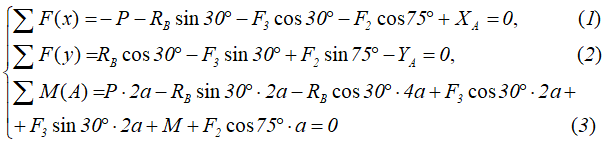
Решая полученную систему уравнений, определяем неизвестные реакции связей катка и шарнирно-неподвижной опоры.

Из уравнения (3) находим реакцию катка

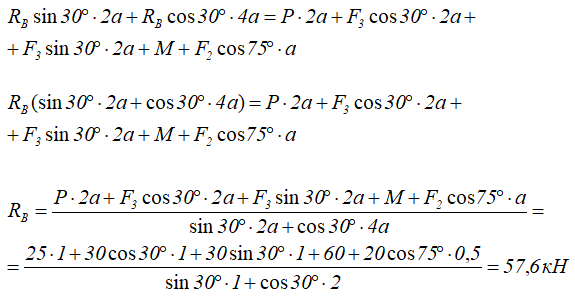
Из уравнения (1) горизонтальную реакцию в точке A

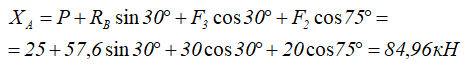
Из уравнения (2) — вертикальную составлюящую реакции связи.

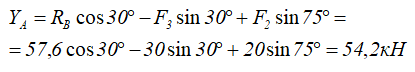
Положительные значения найденных реакций говорят о том, что направление связей было выбрано, верно.

Проверку можно выполнить, составив уравнение суммы моментов, в котором будут записаны все искомые реакции, например, относительно точки D:

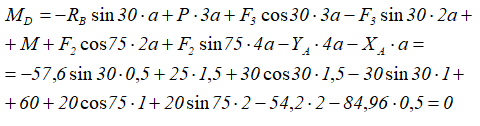
Ноль, полученный в ответе, означает правильность составления и решения уравнений

Ответ: Получены следующие значения сил реакций связей: в катке R_B=57,6кН, в шарнирной опоре X_A=84,96кН и Y_A=54,2кН.

Другие примеры решения задач