Прямоугольную резьбу болта развернем по среднему диаметру в наклонную плоскость, а гайку заменим ползуном.
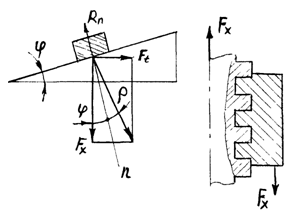
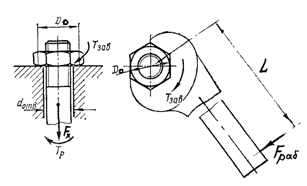
Рисунок 4
Сила взаимодействия наклонной плоскости c ползуном при относительном движении представляет собой равнодействующую нормальной силы и силы трения.
Следовательно, эта сила наклонена к нормали под углом трения ρ. В результате разложения силы получим
где Ft —движущая окружная сила.
Окружная сила трения для витка треугольного профиля:
где f1прив — приведенный коэффициент трения, а приведенный угол трения

Момент завинчивания гаек и винтов
Определим момент трения в резьбе:
При завинчивании гайки к ключу прикладывают момент завинчивания
где L — расчетная длина ключа; Тр — момент в резьбе; Топ — момент трения на опорном торце гайки.
Полезная работа
Затраченная работа равна произведению момента в резьбе на угол поворота в радианах
Таким образом коэффициент полезного действия резьбы
Далее: