Рассмотрим моменты силы относительно точки и относительно оси с примерами расчетов, а также зависимость между ними.

Знание этого вида усилий необходимо для решения задач технической и теоретической механики.

Понятие момента силы

Моментом силы называют вращательное усилие создаваемое вектором силы относительно точки, оси или тела.

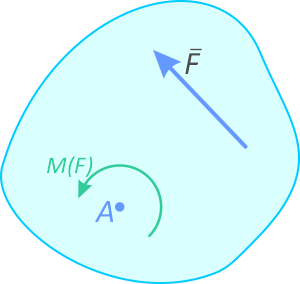
Обозначение: M, m или M(F).

Размерность — [Н·м] (Ньютон на метр) либо кратные значения [кН·м]. Часто размерность записывается без знака умножения [кНм].

Момент силы рассчитывается по формуле:

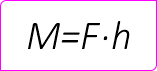
где:
F – величина силы;
h – плечо силы, расстояние от линии её действия до рассматриваемой точки.

Аналогом момента силы является момент пары сил.

Обязательное условие возникновения момента: точка, относительно которой создается момент не должна лежать на линии действия силы.

Определение момента силы

Момент силы определяется произведением силы F на плечо h:

M(F)=F×h

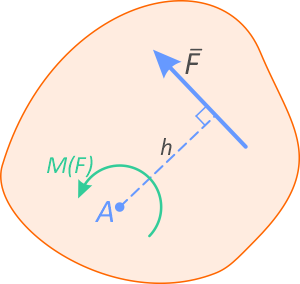
Плечо силы h, определяется как кратчайшее расстояние (по нормали) от точки до линии действия силы.

Например, сила, величиной 7кН, линия действия которой проходит на расстоянии 35см от рассматриваемой точки создает момент

M=7×0,35=2,45кНм.

Пример момента силы

Наиболее наглядным примером момента силы может служить поворачивание гайки гаечным ключом.

Гайки заворачиваются вращением, для этого к ним прикладывается момент, но сам момент в этом случае возникает при воздействии нашей силы на гаечный ключ.

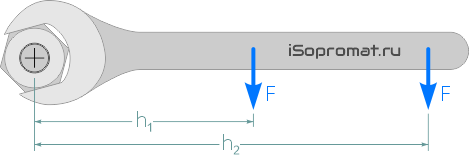
Здесь интуитивно понятно — чтобы сильнее закрутить гайку надо взяться за ключ как можно дальше от нее.

В этом случае, прикладывая ту же силу, получаем большую величину момента за счет увеличения плеча (h2>h1).

Плечом при этом служит расстояние от центра гайки до точки приложения силы.

Плечо момента силы

Рассмотрим порядок определения плеча h момента силы:

Пусть заданы точка A и некоторая произвольная сила F, линия действия которой не проходит через эту точку. Требуется определить момент силы.

Покажем линию действия силы F (штриховая линия)

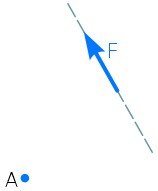
Проведем из точки A перпендикуляр h к линии действия заданной силы

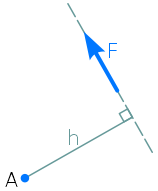
Длина отрезка h есть плечо момента силы F относительно точки A.

Момент принимается положительным, если его вращение происходит против хода часовой стрелки (как на рисунке).

Так принято для того, чтобы совпадали знаки момента и создаваемого им углового перемещения.

Примеры расчета момента силы

Сила расположена перпендикулярно оси стержня

Если сила F приложена перпендикулярно к оси бруса и известно расстояние между точками A и B.

То момент силы F относительно точки A определяется по выражению:

М_A=F×AB

Сила расположена под углом к оси стержня

В случае, если сила F приложена под углом α к оси балки

Момент силы относительно точки B:

M_B=F×cosα×AB

Известно расстояние от точки до линии действия силы

Если известно расстояние от точки где определяется момент до линии действия силы (плечо h)

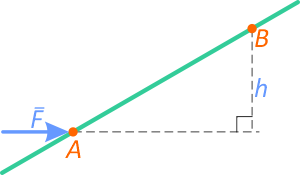
Момент силы относительно точки B:

M_B=F×h

Наш короткий видеоурок про момент силы с примерами:

Другие видео

Момент силы относительно точки

Момент силы относительно точки (или центра) — это вращательный эффект силы, характеризующий вращение твердого тела вокруг некоторой точки под действием приложенной силы.

Определение момента силы относительно точки

Моментом силы относительно точки (рисунок 1) называется векторное произведение радиус-вектора точки приложения силы на вектор силы.

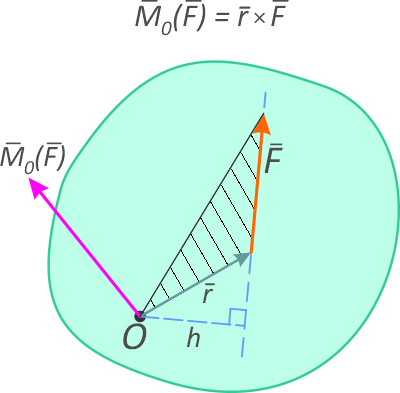
Рисунок 1

Вектор момента направлен перпендикулярно плоскости, в которой лежат сила и точка, в ту сторону, откуда поворот от действия силы виден происходящим против хода часовой стрелки.

Вычисление момента

Вектор момента характеризует положение плоскости и направление вращательного действия силы, а также дает меру этого действия.

Модуль момента силы относительно точки

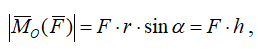
где h – плечо силы (кратчайшее расстояние от точки O – центра момента – до линии действия силы).

Если сила проходит через точку, то ее момент относительно этой точки равен нулю.

Момент силы относительно точки не меняется от переноса силы вдоль линии ее действия.

Если силы расположены в одной плоскости, то используется понятие алгебраического момента силы.

Алгебраическим моментом силы относительно точки (или центра) называется взятое со знаком плюс или минус произведение модуля силы на плечо (рисунок 2).

Правило знаков момента силы относительно точки

Знак плюс выбирается в том случае, если сила стремится поворачивать плоскость относительно центра момента против хода часовой стрелки.

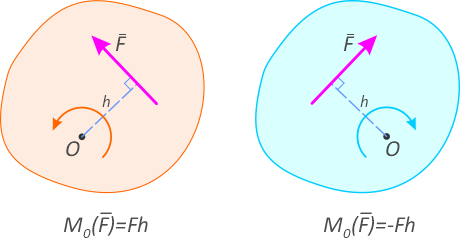
Рисунок 2

Если сила F задана своими проекциями на оси координат F_x, F_y, F_z и даны координаты x, y, z точки приложения этой силы, то момент силы относительно начала координат вычисляется следующим образом:

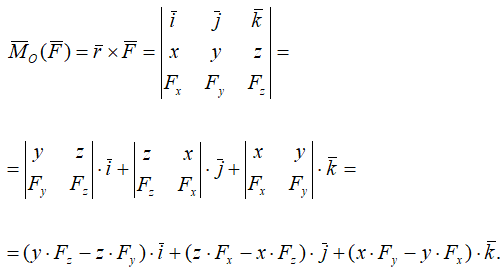
Проекции момента силы на оси координат равны:

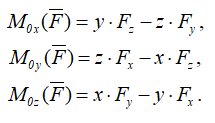
Расчет величины момента силы относительно точки

В общем случае, моментом силы F относительно точки O является результат векторного произведения радиуса-вектора, проведенного из точки O в точку приложения силы, на вектор этой силы:

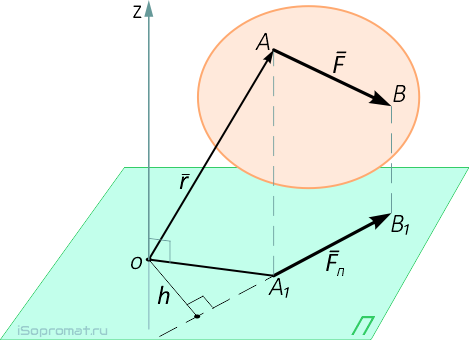
Вектор M_O(F) (рисунок 3) перпендикулярен плоскости, в которой лежат радиус-вектор r и вектор силы F, и направлен так, что если смотреть навстречу ему, видно силу, стремящуюся повернуть плоскость П, в которой она лежит, против хода часовой стрелки.

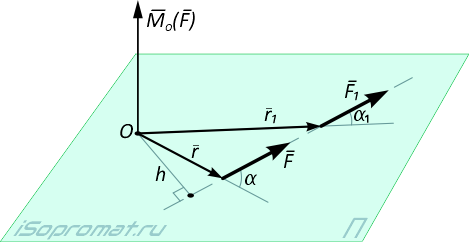
Рисунок 3

Численно момент силы относительно точки равен

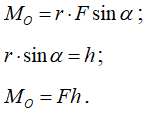
На рисунке 3 видно, что если силу перенести вдоль линии действия в другую точку, то величина и знак момента не изменятся:

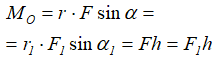
Можно также сказать, что величина момента силы относительно точки равна удвоенной площади треугольника (OAB), основанием которого является сила, а высотой – плечо h (рисунок 4):

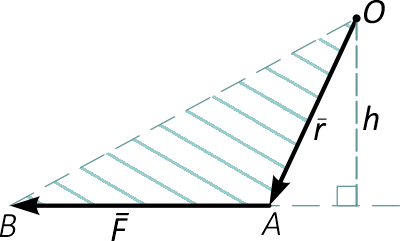
Рисунок 4

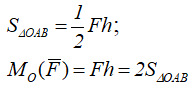
В некоторых случаях для расчета величины момента силы относительно точек удобнее пользоваться теоремой Вариньона.

Пример расчета

К стержню OA длиной 3м, расположенному под углом α=30° в точке A приложена горизонтальная сила F=50Н.

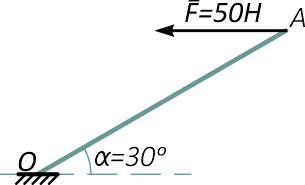
Требуется вычислить момент силы F относительно точки O стержня.

Решение

Определяем плечо силы, проведя нормаль из точки O к линии действия силы F

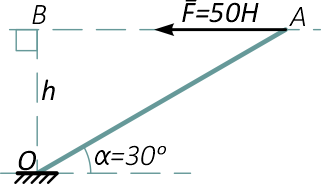
Рассчитаем длину плеча OB

Тогда величина момента силы относительно точки O

По правилу знаков, момент в данном случае положителен.

Момент силы относительно оси

Момент силы относительно оси – алгебраический момент проекции рассматриваемой силы на плоскость, перпендикулярную к оси, относительно точки пересечения оси с этой плоскостью, является характеристикой вращательного действия силы на тело, закрепленное на оси.

Момент силы относительно оси – скалярная величина.

Знаки момента силы относительно оси

Момент считается положительным, если проекция силы на плоскость, перпендикулярную к оси, стремится вращать тело вокруг положительного направления оси против движения часовой стрелки, и отрицательным, если она стремится вращать тело по движению часовой стрелки:

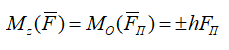
где:
F_П – вектор проекции силы F на плоскость П, перпендикулярную к оси Oz,
точка O – точка пересечения оси Oz с плоскостью П,
h — плечо силы.

Это значит, что момент считается положительным, если мы смотрим навстречу оси и видим проекцию силы, стремящуюся повернуть плоскость чертежа в направлении против хода часовой стрелки.

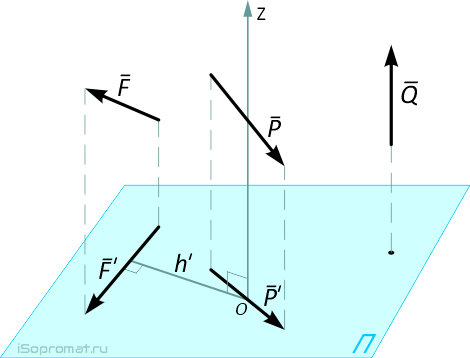
Момент силы F относительно, например, оси Oz, равен алгебраическому моменту проекции этой силы на плоскость, перпендикулярную этой оси (F′) относительно точки пересечения оси с плоскостью, т.е.

Момент силы относительно оси равен нулю, если линия действия силы пересекает ось, т.е. h=0 (например, M_z(P)), или сила параллельна оси, т.е. ее проекция на плоскость равна нулю, например, M_z(Q).

Свойства момента силы относительно оси

Момент силы относительно оси обладает следующими свойствами:

1. момент равен нулю, если сила параллельна оси. В этом случае равна нулю проекция силы на плоскость, перпендикулярную оси;
2. момент равен нулю, если линия действия силы пересекается с осью. В этом случае равно нулю плечо силы.

Другими словами, момент силы относительно оси равен нулю, если сила и ось лежат в одной плоскости.

Моменты силы относительно координатных осей можно получить, расписав векторное произведение

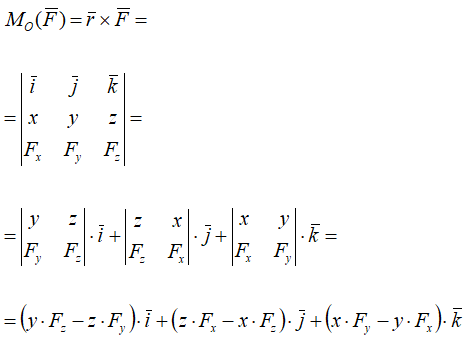
Величины, стоящие в скобках, представляют собой моменты силы F относительно соответствующих осей.

Зависимость моментов силы относительно оси и относительно точки

Рассмотрим зависимость момента силы относительно оси и момента силы относительно точки:

Проведем через точку O, где задан момент силы относительно точки M_O(F) декартовы оси координат x, y и z (рисунок 5).

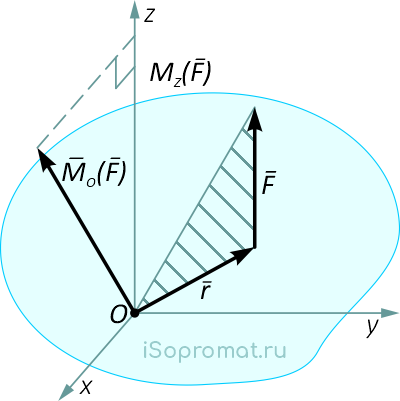
Рисунок 5

Момент силы относительно точки можно представить в виде суммы трех векторов

Эти векторы являются моментами силы относительно осей x, y и z:

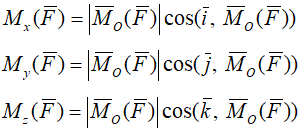
Момент силы относительно оси равен проекции на эту ось момента силы относительно любой точки на оси.

---

Далее: