Рассмотрим общий порядок построения графика (диаграммы) движения толкателя кулачкового механизма:

Закон движения толкателя задан в виде графика ускорений толкателя (при коромысловом толкателе – угловых ускорений).

Однако при дальнейшем решении задачи в качестве аргумента используются не время, а угол поворота кулачка φ.

Другие примеры решений >
Помощь с решением задач >

Поэтому данный график удобно рассматривать как график аналога ускорений S»=f(φ) или ψ»=f(φ) — при коромысловом толкателе.

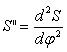
 — аналог ускорения толкателя (линейная величина, пропорциональная ускорению);

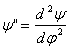
 — аналог углового ускорения коромысла (безразмерная величина, пропорциональная угловому ускорению коромысла).

При дифференцировании графика аналога ускорений соответственно будем получать график аналога скоростей толкателя.

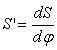
 — аналог скорости толкателя (линейная величина, пропорциональная скорости толкателя);

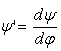
 — аналог угловой скорости коромысла (безразмерная величина, пропорциональная угловой скорости коромысла).

Переход от аналогов к ускорениям или скоростям осуществляется простой заменой переменных через известную угловую скорость кулачка ω₁:

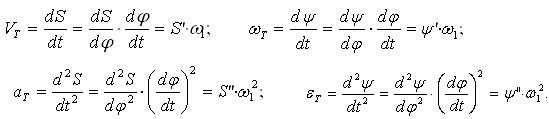
Решение задачи начинается с построения графика аналога ускорений в соответствии с заданием. Выбрав масштаб по оси абсцисс K_φ, отмечаем заданные углы поворота кулачка, соответствующие характерным участкам графика аналога ускорений: 

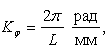
где
L – отрезок на оси абсцисс, соответствующий полному обороту кулачка.

Обычно принимают L=360 мм   (тогда K_φ= 1град/мм = 0,01745рад/мм) или L=240 мм (K_φ=1,5 град/мм=0,0262 рад/мм). 

Ординаты графика аналога ускорений выбираются произвольно, однако площади, ограниченные графиком, над осью и под осью абсцисс должны быть одинаковыми (как на фазе удаления, так и на фазе приближения толкателя).

После построения графика аналога ускорений (аналога угловых ускорений для коромыслового толкателя) производим его интегрирование. Как правило, его производят методом хорд. Для этого:

1) разбиваем каждый характерный участок построенного графика аналога ускорений на более мелкие участки;

2) находим среднее значение функции на выделенных участках (считая, что оно соответствует значению функции на середине выделенного участка) и сносим их на ось ординат;

3) слева от оси ординат на оси абсцисс откладываем полюсное расстояние Н и отмечаем полюс Р (ОР=Н). Полюсное расстояние в принципе назначается произвольно (в пределах 30…60 мм). Однако для дальнейших построений желательно иметь масштабы графиков аналога ускорений, аналога скоростей и перемещений толкателя одинаковыми. В этом случае полюсное расстояние принимается   H = 1/K_φ  (при L=360 мм и 
K_φ= 0,01745 рад/мм – H=57,3 мм; при  L=240 мм и  
K_φ= 0,0262 рад/мм  – H=38,2 мм);

4) соединяя полученные по п. 2 точки на оси ординат с полюсом Р, формируем направления хорд на соответствующих участках графика аналога скоростей;

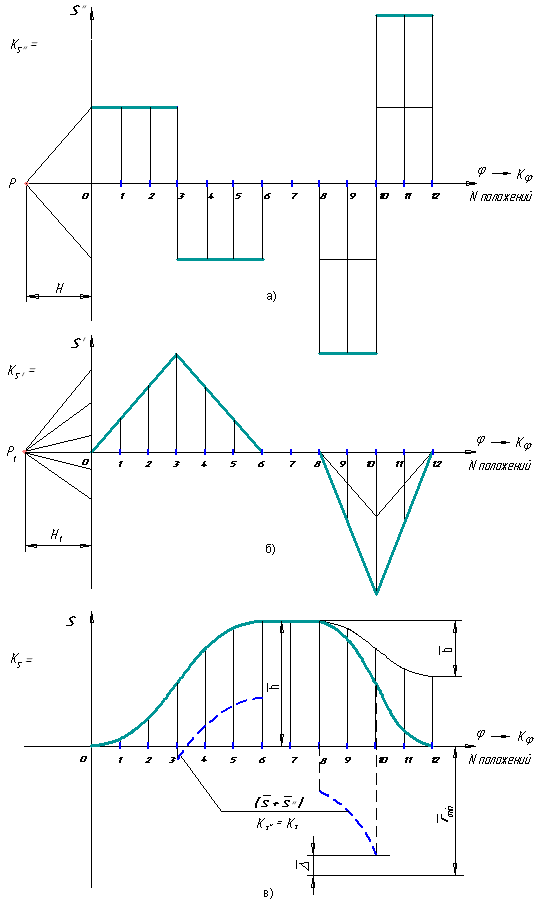
5) из начала координат графика аналога скоростей проводим хорду на первом выделенном участке, далее из конца этой хорды проводим вторую хорду и т.д. Через вершины полученной ломаной кривой проводим плавную кривую, которая и представляет собой график аналога скоростей толкателя (угловых скоростей при коромысловом толкателе).

Аналогичным способом, интегрируя график аналога скоростей, получаем график перемещений толкателя (угловых перемещений при коромысловом толкателе). Может оказаться, что этот график в конце цикла не приходит в «нуль» (т.е. последнее значение перемещений располагается выше или ниже оси абсцисс). 

Но так как на фазе удаления и на фазе приближения толкатель совершает один и тот же путь, то это означает, что левая и правая половина графика изображены в разных масштабах. Поэтому правую часть всех диаграмм (перемещений, аналогов скоростей и аналогов ускорений) надо пропорционально изменить (вытянуть или сжать), умножив на коэффициент μ:

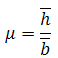
(значения h и b согласно графику перемещения по рисунку 14).

После построения и корректировки всех трех графиков определяем масштабы, в которых они построены:

а) масштаб графика перемещений (угловых перемещений)

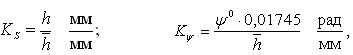
где  h   — заданное перемещение толкателя, мм;
ψ⁰ — заданное перемещение коромысла, град;
_
h  — максимальное значение функции на графике перемещений толкателя (угловых перемещений коромысла);

б) масштаб графика аналога скоростей (аналога угловых скоростей)

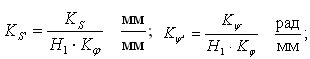
в) масштаб графика аналога ускорений (аналога угловых ускорений)

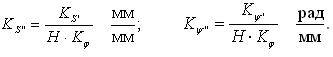
Если приняты рекомендации по пункту 3) данного раздела

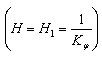
то соответственно масштабы вычисляются следующим образом:

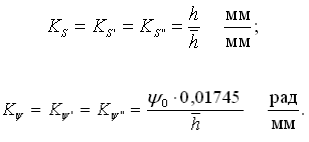
Примечание: Если задан график аналога ускорений в виде простых линий, то ординаты на всех участках этого графика можно определить аналитически из условия, что график  перемещений толкателя в конце цикла должен придти в нуль (см. шаблон пояснительной записки, представленный в Приложении Б).

Кулачковый механизм с поступательно движущимся точечным или роликовым толкателем >
Курсовой проект по ТММ >