Лабораторная работа № 12. Экспериментальное определению перемещения сечения консольной балки при косом изгибе.

Цель работы – определить опытным путем полное перемещение при косом изгибе балки и сравнить его с теоретическим значением.

Основные сведения

Деформация, при которой силы, действующие перпендикулярно оси балки, не лежат в ее главной плоскости, называется косым изгибом.

Возможен плоский косой изгиб, когда внешние силы лежат в одной (силовой) плоскости, и пространственный, когда внешние силы расположены произвольно. В данной работе исследуется плоский косой изгиб.

Балка прямоугольного сечения с главными осями Y и Х повернута так, что вертикальная сила F наклонена к оси X под углом α (рис. 12.1). Раскладывая силу F на две составляющие F_x и F_y, получим два поперечных изгиба силами F_x= F∙cos α и F_у = F∙sin α.

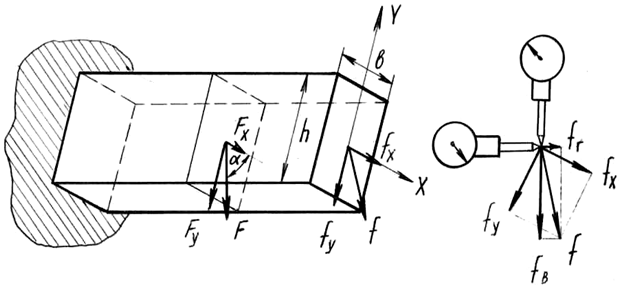
По принципу независимости действия сил можно определить в любом сечении составляющие каждого прогиба, в данном случае f_x и f_y. Аналитически это удобнее проделать по способу Верещагина.

В работе опытным путем определяются вертикальные и горизонтальные перемещения f_в и f_г. Полный прогиб является геометрической суммой прогибов по любым взаимно перпендикулярным направлениям, следовательно,

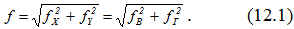
Порядок выполнения и обработка результатов

Исследования деформации косого изгиба выполняются на специальной настольной установке СМ-8 м (рис. 12.2).

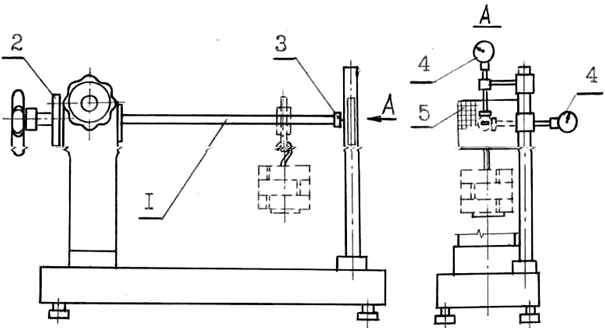
Рис. 12.2. Схема установки СМ-8 м

Установка смонтирована на массивной опоре с устройством для поворота и жесткого закрепления образца. Образец I – балка прямоугольного сечения размером 7х32 мм². Угол поворота устанавливается по шкале 2 в пределах 0 ± π/2. На конце образца закреплена втулка с иглой 3 для визуального наблюдения за перемещением балки по прозрачному экрану 5 с сеткой.

Точное измерение составляющих полного перемещения f_в и f_г конечного сечения производится двумя индикаторами часового типа 4 со специальными удлинителями и пятками. Кстати, при круговом повороте балки вокруг оси игла 3 описывает эллипс с — главными полуосями, равными прогибам при угле поворота 0 и π/2.

Доказать это предлагается любознательным студентам самостоятельно, в свободное от других занятий время. Нагружение балки проводится несколькими ступенями с регистрацией составляющих прогиба f_в и f_г, анализируется линейная зависимость их от нагрузки.

По окончании работы образец разгружается и показания индикаторов сверяются с начальными. Записи показаний индикаторов и вычисления полного прогиба заносят в журнал испытаний, определяя при этом погрешность

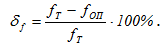
Контрольные вопросы

Испытание на внецентренное нагружение >
Другие лабораторные работы >
Примеры решения задач >