Формулы для расчета осевых Ix, Iy и полярных IΡ моментов инерции плоских фигур и сечений
Для произвольной фигуры площадью A с элементарной площадкой dA:
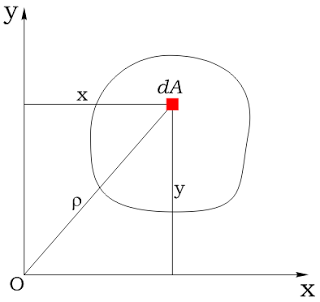
Осевые моменты инерции относительно осей x и y:
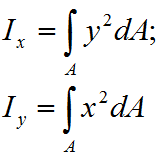
Полярный момент инерции относительно т. O:
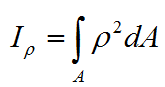
Учитывая то, что:
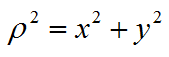
видим, что полярный момент инерции сечения равен сумме осевых:
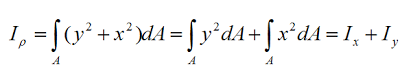
Моменты инерции измеряются в [м4].
Далее: