Моменты инерции плоских сечений и фигур относительно смещенных осей рассчитываются по формулам:

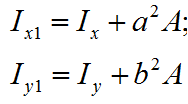
Здесь:
I_x, I_y — осевые моменты инерции фигур;
a, b — смещение осей вдоль y и x;
A — площадь сечения фигур.

Рассмотрим плоское сечение произвольной формы площадью A.

Выделим в нем элементарную площадку dA с координатами x и y относительно системы координат проходящей через центр тяжести сечения O:

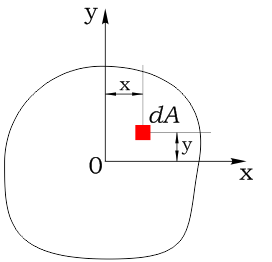
Покажем новую систему координат, y₁O₁x₁, отстоящую от осей x и y первой системы на a и b соответственно

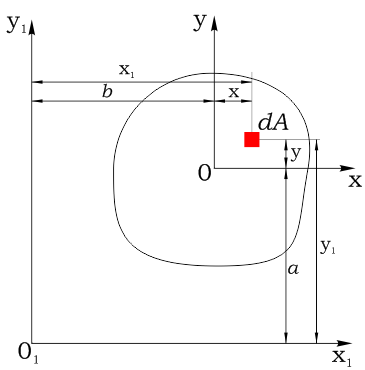
Новое положение элементарной площадки после смещения осей:

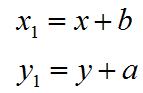
Осевые моменты инерции относительно смещенных осей x₁ и y₁.

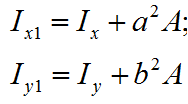
Здесь I_x и I_y — осевые моменты инерции сечения.

Далее: