Мгновенным центром ускорений (сокр. — МЦУ) при движении фигуры в плоскости называют точку плоской фигуры, ускорение которой в этот момент равно нулю.
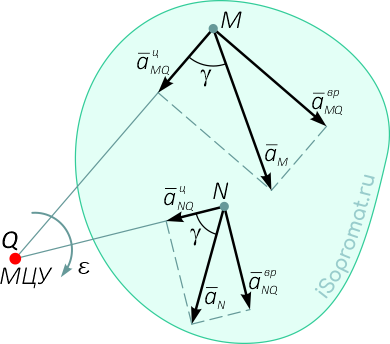
Такая точка существует в каждый момент времени движения фигуры и твердого тела и на схемах обозначается буквой Q.
Взяв эту точку за полюс, и учитывая что
![]()
получим формулу для определения ускорения произвольной точки:
![]()
или
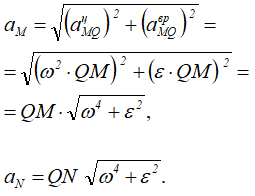
Угол, который составляет вектор ускорения точки М с линией MQ определится из соотношения:
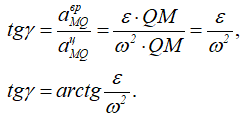
Т.е. в каждый момент времени, у всех точек плоской фигуры этот угол одинаков.
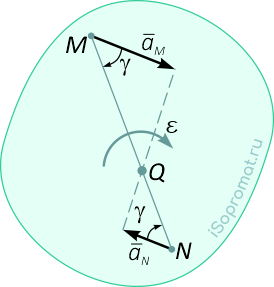
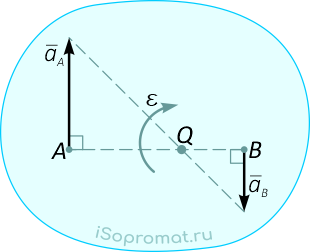
На рисунке 1 видно, что МЦУ фигуры лежит в точке пересечения линий, составляющих угол γ с соответствующими ускорениями точек.
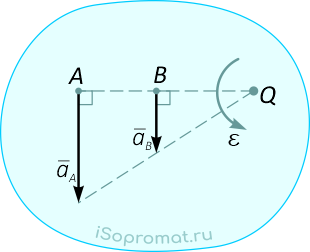
На следующих рисунках приведены частные случаи определения положения мгновенного центра ускорений.
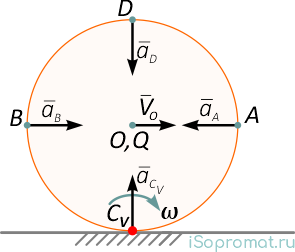
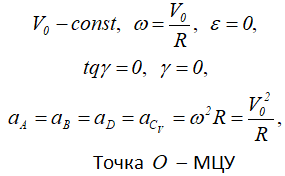
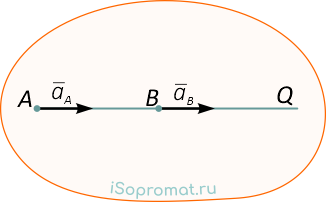
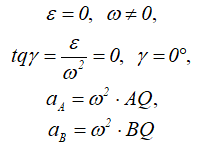
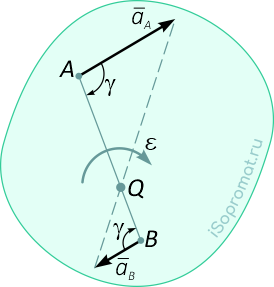
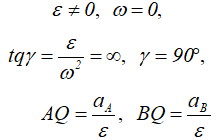
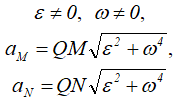
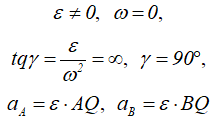
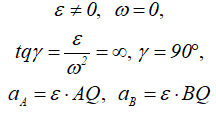
Далее: