Для некоторых видов движения фигур и твердых тел положение мгновенного центра ускорений определяется достаточно просто.
Такие случаи называют частными.
Примеры частных случаев положения МЦУ:
1.
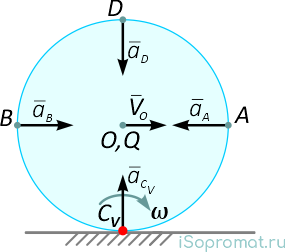
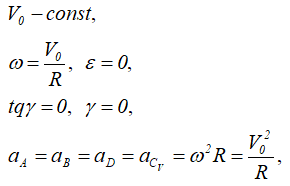
Здесь, мгновенный центр ускорений находится в центре колеса в точке O.
2.
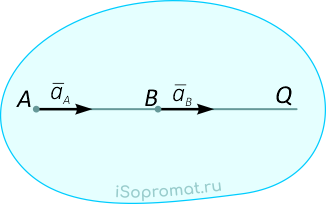
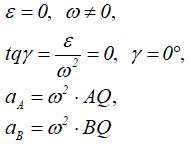
3.
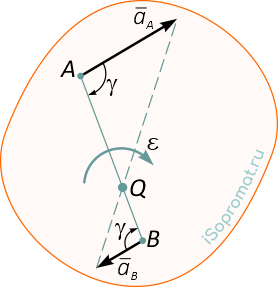
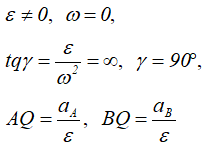
4.
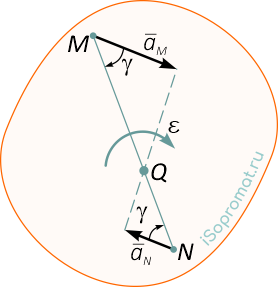
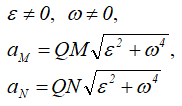
5.
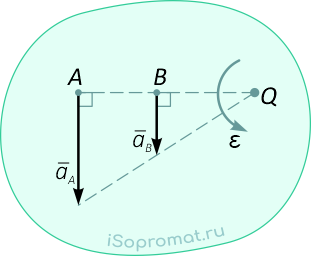
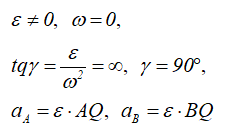
6.
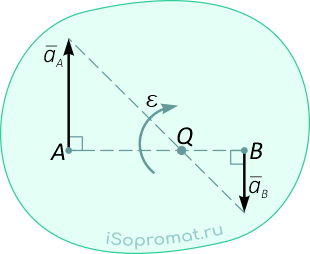
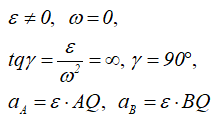
Далее: