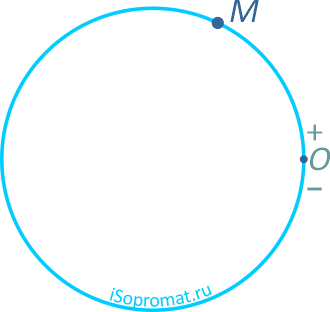
Пример решения задачи по определению в заданный момент времени угла между вектором ускорения точки, движущейся по траектории окружности и радиусом этой окружности.
Задача
Точка движется по окружности радиуса R по закону: S=2πRt2.
Требуется, в момент времени
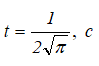
определить угол между вектором ускорения и радиусом.
Решение
Движение точки задано естественным способом: известна траектория (окружность) и закон движения точки по этой траектории.
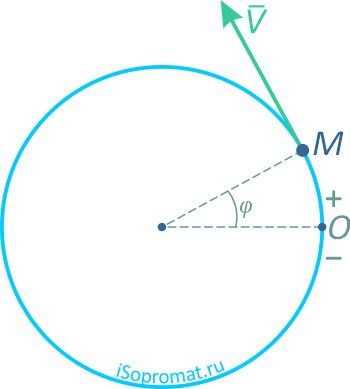
Выбрав начало отсчета и положительное направление движения, показываем положение точки в заданный момент времени:
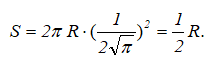
При длине дуги R/2 центральный угол составит φ=S/R=1/2 рад.
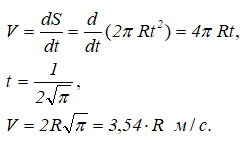
Вектор скорости направлен по касательной к траектории движения, в сторону возрастания дуговой координаты.
Касательное, нормальное и полное ускорения точки:
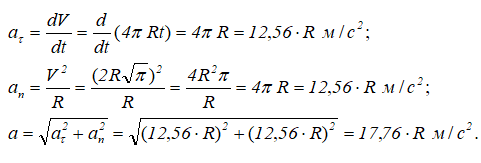
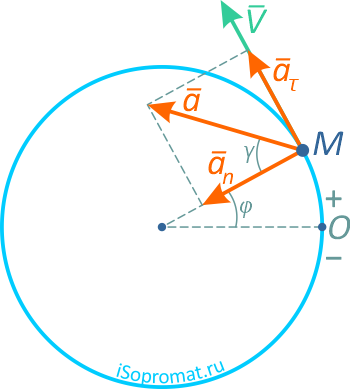
Покажем их направление
Угол между вектором ускорения и радиусом :
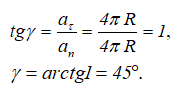
Далее: