Скорость точки — кинематическая мера её движения, равная производной по времени от радиус-вектора этой точки в рассматриваемой системе отсчета.

Скорость относительно выбранной системы отсчета это одна из основных кинематических характеристик движения точки.

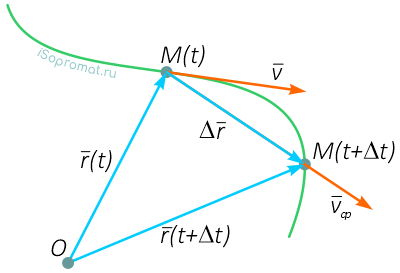
Вектор скорости направлен по касательной к траектории точки в сторону движения.

Рассмотрим перемещение точки за малый промежуток времени Δt:

тогда средняя скорость точки за промежуток времени Δt

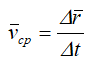
Скорость точки в данный момент времени

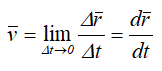
Видеоурок по теме:

Другие видео

Рассмотрим подробнее определение скорости движения материальной точки при различных способах задания ее движения.

Скорость точки при векторном способе задания движения

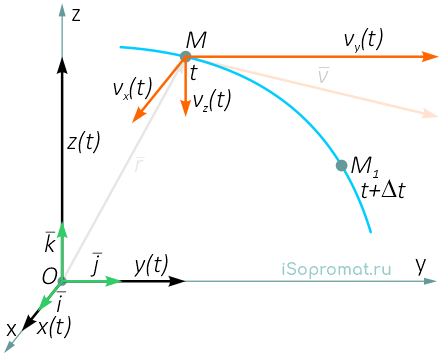
При векторном способе задания движения положение движущейся точки М относительно системы отсчета в момент времени t₁ определяется радиус-вектором r

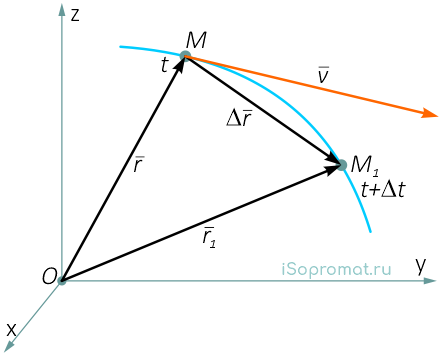
В другой момент времени t₁=t+Δt точка займет положение М₁ с радиус-вектором r₁.

За время Δt радиус-вектор движущейся точки изменится на

Средней скоростью v_ср называется отношение изменения радиус-вектора Δr к изменению времени Δt.

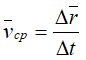
Скорость точки равна первой производной по времени от ее радиус-вектора.

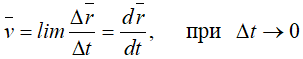
Скорость точки при координатном способе задания движения

При координатном способе задания движения перемещение материальной точки определяется уравнениями.

Разложим радиус-вектор и скорость на составляющие, параллельные осям координат

Получим следующие выражения

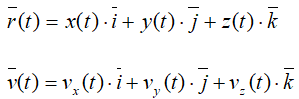
После дифференцирования получается зависимость

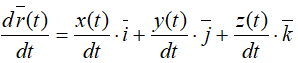
Откуда следует

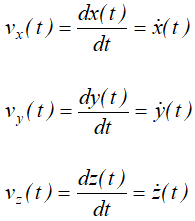
Проекция скорости точки на какую-либо координатную ось равна первой производной по времени от соответствующей координаты этой точки.

Модуль скорости и направляющие косинусы равны:

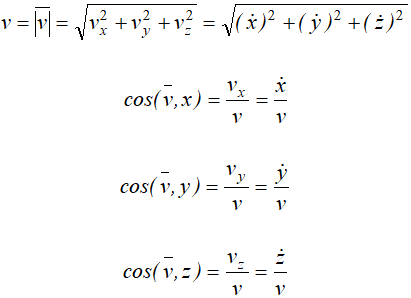
Если материальная точка движется в плоскости, то, выбрав оси координат Ox и Oy в этой плоскости, получим:

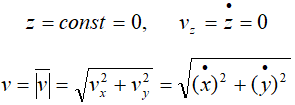
Для прямолинейного движения точки координатную ось, например ось Ox, направляем по траектории.

Тогда

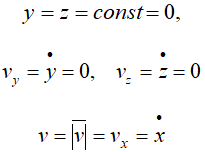
Скорость точки при естественном способе задания движения

Пусть скорость материальной точки задана естественным способом, т.е. заданы траектория точки и закон ее движения по траектории s=f(t).

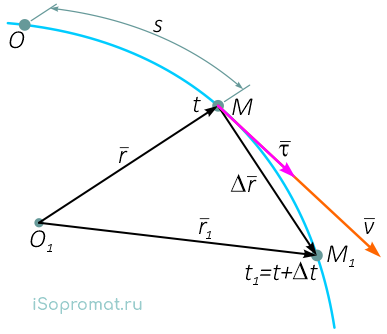
Вычислим скорость точки. Используем радиус-вектор r. движущейся точки, начало которого находится в неподвижной точке O₁

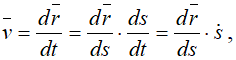
где

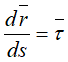
— единичный вектор, направленный по касательной к траектории в сторону возрастающих расстояний.

При ds>0 направления векторов τ и dr совпадают.

Если точка движется в сторону убывающих расстояний, то ds<0 и направления векторов τ и dr противоположны.

При

вектор скорости направлен по τ, т.е. в сторону возрастающих расстояний;

При

он имеет направление, противоположное τ, т.е. в сторону убывающих расстояний.

Здесь

— алгебраическая скорость точки, проекция скорости v на положительное направление касательной к траектории.

Естественное задание движения точки полностью определяет скорость по величине и направлению.

---

Далее: