Пример решения задачи по определению ускорения точки, находящейся в середине дуги окружности обода движущегося диска заданного радиуса по известным ускорениям двух точек, лежащих на диаметре диска.

Задача

В плоскости xOy движется диск радиуса R=20 cм. Известны ускорения двух точек, лежащих на диаметре диска: a_A=40 см/с² и a_B=20 см/с². Их направления указаны на рисунке 2.38: α=90°, β=30°.

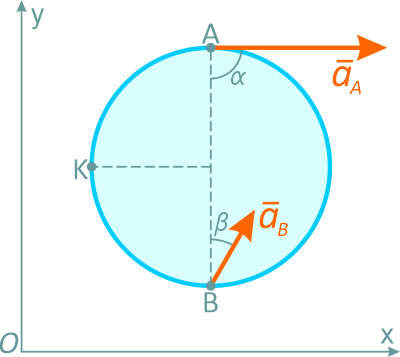
Требуется определить ускорение точки K, лежащей в середине дуги окружности AB обода диска.

Решение

Для определения угловой скорости и углового ускорения диска напишем формулу для ускорения точки B, взяв за полюс точку A:

В этой формуле два вектора ускорений точки A a_A и a_B полностью известны, у векторов a_BA^ц и a_BA^вр неизвестны величины, но известны направления: вектор a_BA^ц направлен от B к точке A, т.е. он перпендикулярен вектору a_A, а вектор a_BA^вр перпендикулярен отрезку AB и вектору a_BA^ц. Следовательно, это векторное равенство можно построить (рисунок 2.39).

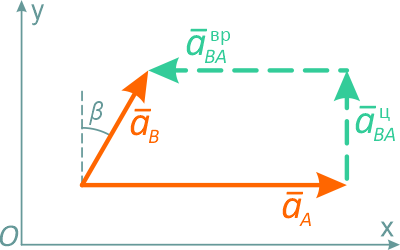
Спроецировав равенство на выбранные оси координат, получим два выражения:

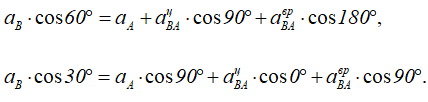
Решая эти выражения, получим:

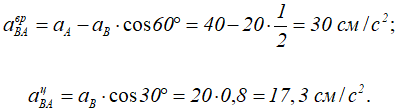
Учитывая, что

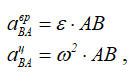
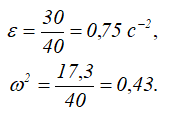
Направление вектора a_BA^вр показывает, что угловое ускорение диска направлено по ходу часовой стрелки.

Для определения ускорения точки, движущейся по дуге окружности K запишем формулу

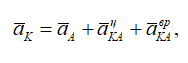
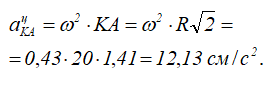
Этот вектор направлен от точки K к точке Α.

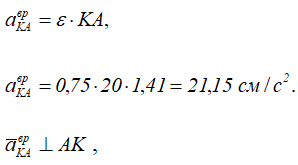
его направление определяется направлением углового ускорения диска.

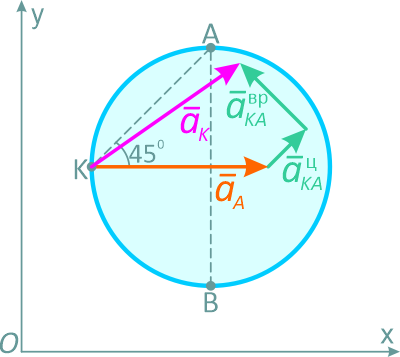
На рисунке 2.40 показано геометрическое сложение векторов, определяющих ускорение точки K. Все составляющие известны по величине и направлению. Поэтому, построив в масштабе векторный многоугольник, можно определить величину и направление ускорения точки K.

Для выполнения аналитических расчетов формулу, определяющую ускорение точки K, проецируем на выбранные оси:

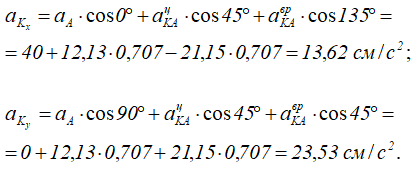
Полное ускорение точки K:

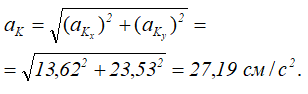
Направление вектора a_K определяют углы, которые он составляет с осями координат:

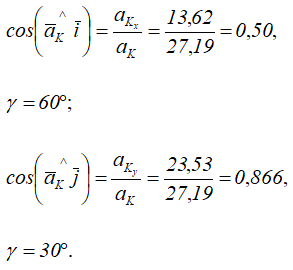
Решение задачи завершено.

---

Далее: