Пример решения задачи технической и теоретической механики по определению траектории равноускоренного движения точки, заданного уравнениями, скорости и ускорения в заданные моменты времени, координаты начального положения точки, а также путь, пройденный точкой за время t.
Задача
Движение точки A задано уравнениями:
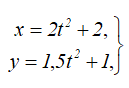
где координаты x и y – в сантиметрах [см], а время t – в секундах [с]. Определить траекторию движения точки, скорость и ускорение в моменты времени t0=0 с, t1=1 с и t2=5 с, а также путь, пройденный точкой за время равное 5 с.
Решения других задач
Помощь с решением
Решение
Определение траектории движущейся точки
Определяем траекторию точки. Умножаем первое заданное уравнение на 3, второе – на (-4), а затем складываем их левые и правые части:
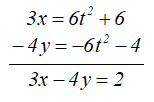
Получилось уравнение первой степени – уравнение прямой линии, значит движение точки – прямолинейное (рисунок 1.5).
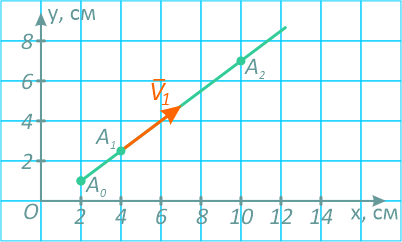
Для того, чтобы определить координаты начального положения точки A0, подставим в заданные уравнения значения t0=0; из первого уравнения получим x0=2 см, из второго y0=1 см.
При любом другом значении t координаты x и y движущейся точки только возрастают, поэтому траекторией точки служит полупрямая 3x-4y=2 с началом в точке A0 (2; 1).
Пример расчета кинематических параметров точки движущейся по криволинейной траектории.
Определение скорости движения точки
Определяем скорость движения точки, найдя сначала ее проекции на оси координат:
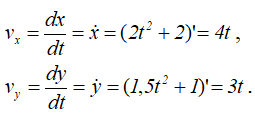
тогда полная скорость движущейся точки
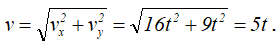
При t0=0с скорость точки v0=0, при t1=1с v1=5 см/с, при t2=5с v2=25см/с.
Определение ускорения движущейся точки
Определяем ускорение точки. Его проекции на оси координат:
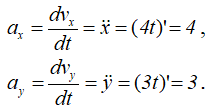
Проекции ускорения не зависят от времени движения,
т.е. движение точки равноускоренное, векторы скорости и ускорения совпадают с траекторией точки и направлены вдоль нее.
С другой стороны, поскольку движение точки прямолинейное, то модуль ускорения можно определить путем непосредственного дифференцирования уравнения скорости:
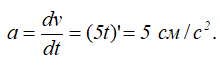
Определение пути пройденного точкой
Определяем путь, пройденный точкой за первые 5 секунд движения. Выразим путь как функцию времени:
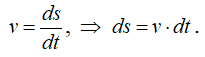
Проинтегрируем последнее выражение:
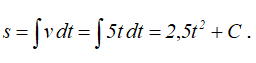
Если t=t0=0, то C=s0; в данном случае s0=0, поэтому s=2,5t2.
Находим, что за 5 секунд точка проходит расстояние
s|t=5с=2,5∙52=62,5см.
Кинематические параметры движения точки прямолинейного и равноускоренного движения точки определены.
Дополнительно:
