Варианты заданий с 1 по 10 к РГР Д19 по теоретической механике для студентов очной, заочной и дистанционной форм обучения.

Вариант №1

Механическая система, состоящая из груза 1, невесомой нерастяжимой нити и однородного блока 2, вращающегося вокруг неподвижной оси, приводится в движение силой F.

При заданных величинах:
m₁=6 кг, f = 2/10√3, a₁=4 м/с², α=30°,
m₁=8 кг, R₂=0,2 м, M=0,8 Нм
определить:

1. работу силы трения при перемещении груза 1 на величину s=1 м;
2. главный момент сил инерции блока 2;
3. натяжение нити между грузом и блоком;
4. величину силы F;
5. при какой максимальной величине силы F система будет находиться в равновесии.

Вариант №2

Механическая система состоит из однородного блока 2, вращающегося вокруг неподвижной оси, невесомой нерастяжимой нити и катка 1, скатывающегося вниз по наклонной плоскости.

При заданных величинах:
m₁=9 кг, δ=0,04/√3 м, R₁=0,4 м, r₁=0,2 м,
a₁=2  м/с², R₂=0,2 м, α=30°, i₁=0,2
определить:

1. работу момента сопротивления качению катка 1 при перемещении его точки O на величину s=2 м;
2. главный момент сил инерции катка 1;
3. натяжение нити между катком и блоком;
4. массу блока 2;
5. при каком наименьшем моменте, приложенном к блоку 2, система будет уравновешена.

Вариант №3

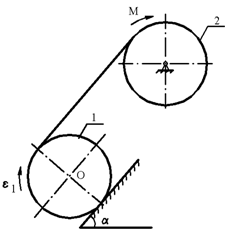
Система, состоящая из однородного блока 2, вращающегося вокруг неподвижной оси, невесомой нерастяжимой нити и однородного катка 1, перемещающегося вверх по плоскости, наклоненной под углом α к горизонту, приводится в движение моментом M.

При заданных величинах:
m₁=2 кг, δ₁=1/5√3 м, m₂=2 кг, R₁=1 м,
R₂=2 м, α=30°, ε=2 c^-2
определить:

1. главный вектор сил инерции катка 1;
2. главный момент сил инерции катка 1;
3. натяжение нити между катком 1 и блоком 2;
4. величину момента M, приложенного к блоку 2;
5. работу момента сопротивления качению при прохождении точкой O катка 1 пути s=1 м.

Вариант №4

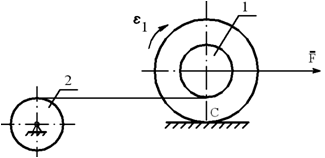
Механическая система, состоящая из вала 1 с барабаном, невесомой нерастяжимой нити и однородного блока 2, вращающегося вокруг неподвижной оси, приводится в движение силой F. Проскальзывание в точке C отсутствует.

При заданных величинах:
m₁=8 кг, δ=0,006 м, R₁=0,6 м, r₁=0,2 м,
ε₁=4 с^-2, R₂=0,25 м, m₂=6 кг, i₁=0,3 м
определить:

1. работу момента сопротивления качению при повороте вала с барабаном на угол φ=100 радиан;
2. главный момент сил инерции блока 2;
3. натяжение нити между блоком и валом;
4. величину силы F;
5. какой величины момент достаточно приложить к блоку 2, чтобы система была уравновешенной.

Вариант №5

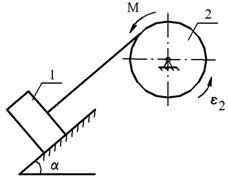
При действии момента M система, состоящая из однородного блока 2, вращающегося вокруг неподвижной оси, невесомой нерастяжимой нити и груза 1, перемещающегося по плоскости, наклоненной к горизонту под углом α, приводится в движение.

При заданных величинах:
m₁=4 кг, m₂=8 кг, R₂=√2 м,
ε₂=1 c^-2, M=60 Нм, α=45°
определить:

1. главный вектор сил инерции груза 1;
2. главный момент сил инерции блока 2;
3. натяжение нити между блоком и грузом;
4. величину коэффициента трения скольжения f;
5. при какой величине момента M система при f=0,2 будет находиться в равновесии.

Вариант №6

Система, состоящая из однородного блока 2, вращающегося вокруг неподвижной оси, невесомой нерастяжимой нити и катка 1, перемещающегося вверх по плоскости, наклоненной к горизонту под углом α, приводится в движение моментом M, приложенным к блоку 2.

При заданных величинах:
m₁=2 кг, δ=1/2√3, R₁=2 м, r₁=1 м,
m₂=1/9 кг, R₂=4 м, α=30°, i₁=1 м, ε₂=9 c^-2
определить:

1. главный вектор сил инерции катка 1;
2. главный момент сил инерции катка 1;
3. натяжение нити между блоком 2 и катком 1;
4. момент M, приводящий систему в движение;
5. какой величины должен быть момент M, чтобы система находилась в равновесии.

Вариант №7

При действии момента M система, состоящая из вращающегося однородного блока 2, невесомой нерастяжимой нити и катка 1, перемещающегося вверх по плоскости, составляющей угол α с горизонтом, приводится в движение.

При заданных величинах:
m₁=3 кг, δ=1/√3 м, R₁=2 м, r₁=1 м,
i₁=1 м, ε₂=6 c^-2, R₂=2 м, α=30°
определить:

1. величину работы момента сопротивления качению, приложенного к катку 1, при повороте его на угол φ=2 радиана;
2. главный вектор сил инерции катка 1;
3. натяжение нити между катком и блоком;
4. массу блока 2;
5. натяжение нити между катком и блоком при равновесии системы в случае уменьшения величины момента М.

Вариант №8

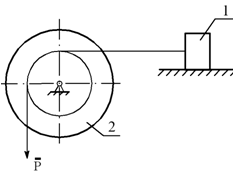
Система, состоящая из вала с барабаном 2, вращающегося вокруг неподвижной оси, невесомой нерастяжимой нити и груза 1, перемещающегося по негладкой горизонтальной плоскости, приводится в движение силой P.

При заданных величинах:
m₁=0,2 кг, m₂=0,3 кг, R₂&=4 м, r₂=2 м,
a₁=4 м/c², f=0,1, i₂=4 м
определить:

1. главный момент сил инерции барабана 2;
2. главный вектор сил инерции барабана 2;
3. натяжение нити между грузом 1 и блоком 2;
4. величину силы P;
5. максимальную величину силы P, при которой система останется в покое.

Вариант №9

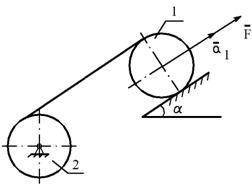
Механическая система, состоящая из однородного катка 1, невесомой нерастяжимой нити и однородного блока 2, вращающегося вокруг неподвижной оси, приводится в движение силой F.

При заданных величинах:
m₁=4 кг, δ₁=8/100√3 м, R₁=0,2 м, m₂=8 кг,
a₁=1 м/c², R₂=0,2 м, α=30°
определить:

1. главный вектор сил инерции катка 1;
2. главный момент сил инерции блока 2;
3. работу момента сопротивления при качении катка 1 при повороте его на угол φ=10 радиан;
4. величину силы F;
5. при какой наибольшей величине силы F система будет находиться в покое.

Вариант №10

Механическая система, состоящая из однородного блока 2, вращающегося вокруг неподвижной оси, невесомой нерастяжимой нити, вала с барабаном 1, перемещающегося по горизонтальным направляющим, приводится в движение моментом M.

При заданных величинах:
m₁=2 кг, δ=0,4 м, R₁=2 м, r₁=1 м,
ε₁=4 c^-2, m₂=12 кг, M=72 Нм, i₁=2 м
определить:

1. главный вектор сил инерции барабана 1;
2. главный момент сил инерции барабана 1;
3. натяжение нити между барабаном 1 и блоком 2;
4. величину радиуса R₂ блока 2;
5. работу момента сопротивления качению барабана 1 при повороте его на угол φ=2 рад.

---