Вывод формул и зависимостей для определения положения центров тяжести простых фигур — треугольника, дуги окружности и кругового сектора.
Центр тяжести треугольника
Центр тяжести площади треугольника совпадает с точкой пересечения его медиан (рисунок 1).
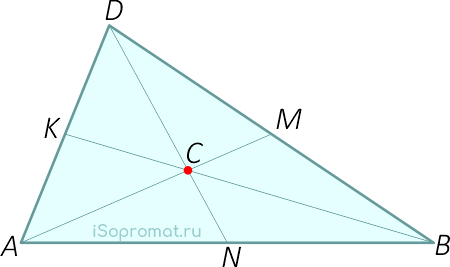
Отсюда зависимость отрезков и положение точки C:
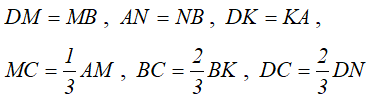
Центр тяжести дуги окружности
Дуга имеет ось симметрии (рисунок 2).
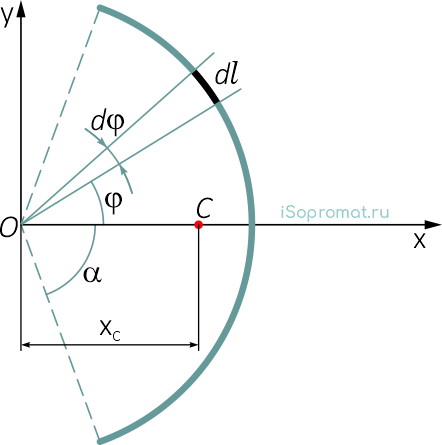
Центр тяжести лежит на этой оси, т.е. yC = 0.
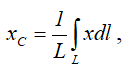
dl – элемент дуги,
![]()
R – радиус окружности,
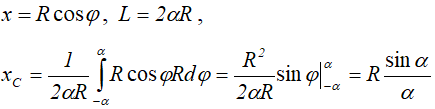
Следовательно:
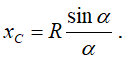
Центр тяжести кругового сектора
Сектор радиуса R с центральным углом 2α имеет ось симметрии Ox, на которой находится центр тяжести (рисунок 3).
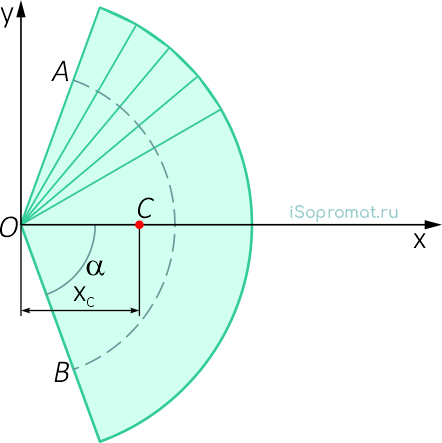
Разбиваем сектор на элементарные секторы, которые можно считать треугольниками. Центры тяжести всех элементарных секторов располагаются на дуге окружности радиуса 2R/3.
Центр тяжести сектора совпадает с центром тяжести дуги AB:
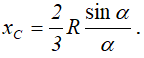
Далее: