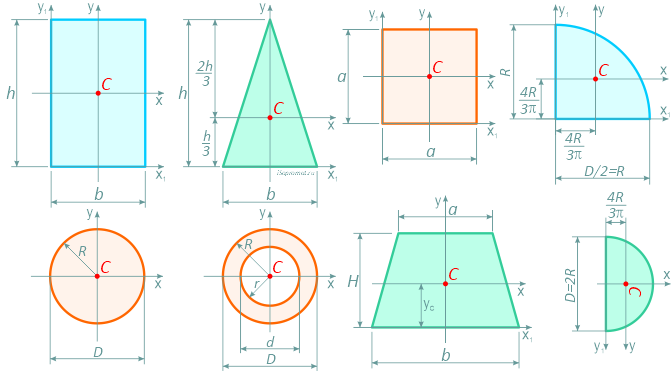
Формулы определения площадей, центров тяжести, осевых и полярных моментов инерции, моментов сопротивления и других геометрических характеристик основных фигур: прямоугольника, квадрата, равнобедренного и прямоугольного треугольника, круга, полукруга, четверти круга, кольцевого и тонкостенного (трубного) сечений.
Обозначения в формулах:
C — положение центра тяжести фигуры;
A — площадь сечения;
Ix , Iy — осевые моменты инерции сечения относительно главных осей;
Ix1 , Iy1 — осевые моменты инерции относительно вспомогательных (смещённых) осей;
Iρ — полярный момент инерции сечения;
Wx , Wy — осевые моменты сопротивления относительно осей x и y;
Wρ — полярный момент сопротивления.
Прямоугольник
Геометрические характеристики прямоугольника высотой h и шириной b.
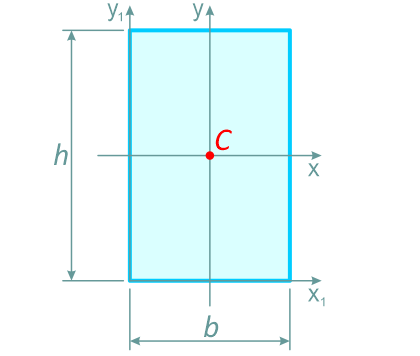
Центр тяжести прямоугольника расположен в точке пересечения его диагоналей, на расстоянии половины высоты (h/2) по вертикали и половины ширины (b/2) по горизонтали.
Площадь
![]()
Центральные осевые моменты инерции прямоугольника определяются по формулам
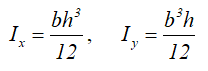
Моменты инерции относительно смещенных осей, проходящих через нижнюю левую точку
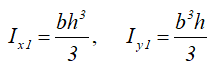
Осевые моменты сопротивления прямоугольного сечения
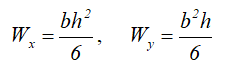
Квадрат
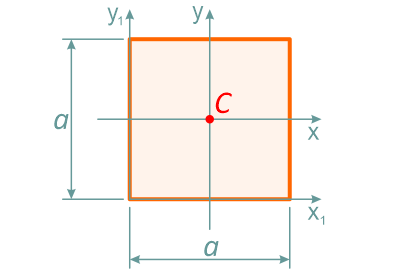
Квадрат — это частный случай прямоугольника, у которого высота равна ширине, т.е. h=b=a.
Центр тяжести квадрата находится так же на пересечении диагоналей — на расстоянии половины стороны (a/2) по высоте и ширине.
Площадь
![]()
Центральные осевые моменты инерции квадрата
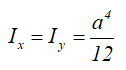
Моменты инерции относительно смещенных осей, проходящих через нижнюю левую точку вычисляются по формуле
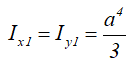
Осевой момент сопротивления квадратного сечения
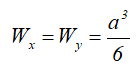
Треугольник равнобедренный
Равнобедренный треугольник высотой h и шириной основания b.
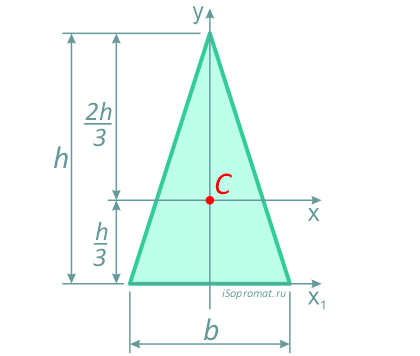
Центр тяжести треугольника располагается в точке пересечения его медиан на расстоянии 1/3 высоты от основания и 2/3 высоты от его вершин.
Площадь
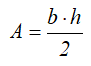
Центральные осевые моменты инерции треугольника
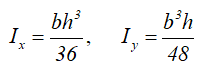
Момент инерции относительно смещенной оси x1, проходящей через его основание
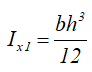
Прямоугольный треугольник
Прямоугольный треугольник высотой h и шириной основания b.
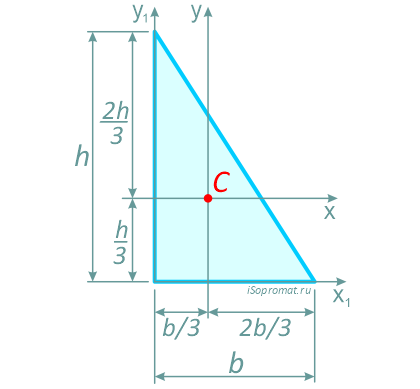
Центр тяжести прямоугольного треугольника располагается аналогично, на пересечении медиан на расстоянии 1/3 высоты от основания и 2/3 высоты от вершины.
Площадь
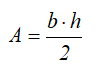
Центральные осевые моменты инерции прямоугольного треугольника
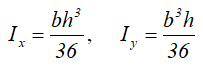
Моменты инерции относительно смещенных осей x1 и y1, проходящих через точку, соединяющую его катеты
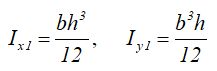
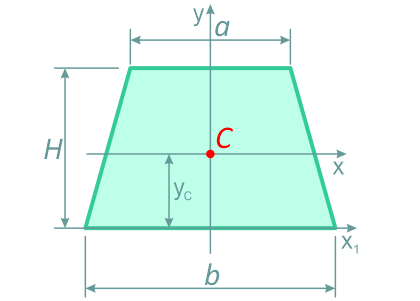
Трапеция
Равнобокая трапеция высотой H и шириной оснований: малого a и большого b.
Площадь трапеции
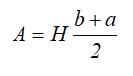
Центр тяжести на линии, соединяющей середины оснований трапеции, на высоте, определяемой по формуле:
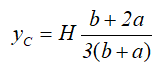
Круг
Круг диаметром D (d) или радиусом R (r)
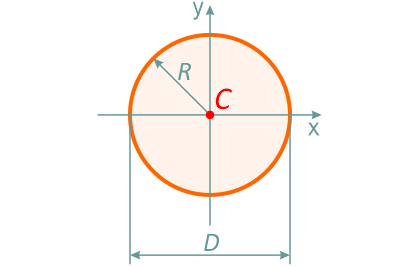
Площадь круга через его диаметр и радиус
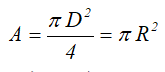
Центральные осевые и полярный моменты инерции круга
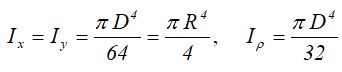
Осевые и полярный моменты сопротивления
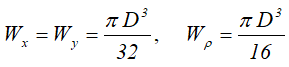
Полукруг
Половина круга диаметром D (d) или радиусом R (r)
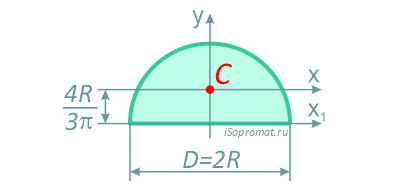
Площадь
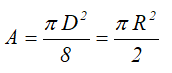
Осевые моменты инерции полукруга
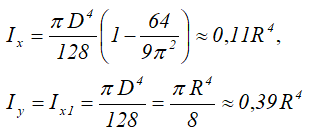
Четверть круга
Четверть круга диаметром D (d) или радиусом R (r)
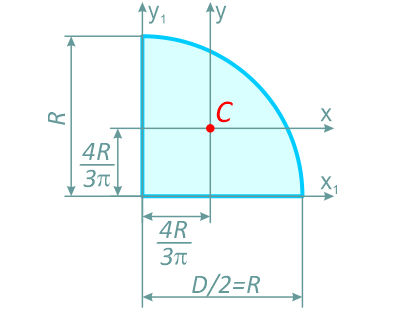
Площадь
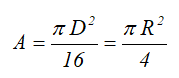
Центральные осевые моменты инерции четверти круга
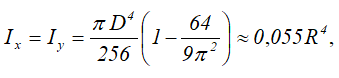
Моменты инерции относительно смещенных осей x1 и y1
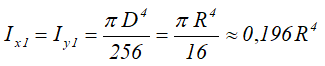
Кольцо
Кольцо с внешним диаметром D и внутренним d, (радиусами: внешним R и внутренним r)
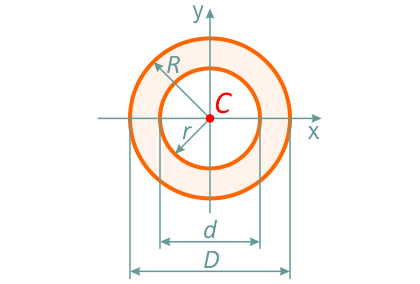
Отношение внутреннего диаметра (радиуса) к внешнему обозначается буквой c.
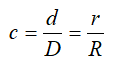
Площадь
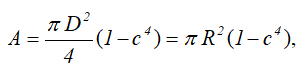
Центральные осевые и полярный моменты инерции кольца
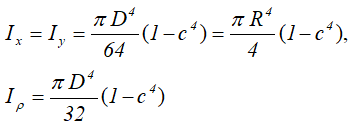
Осевые и полярный моменты сопротивления
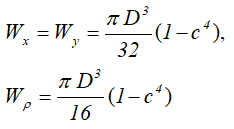
Тонкостенное сечение (труба)
Тонкостенный профиль (сечение трубы) средним радиусом R0 и толщиной стенки трубы t при t<<R0
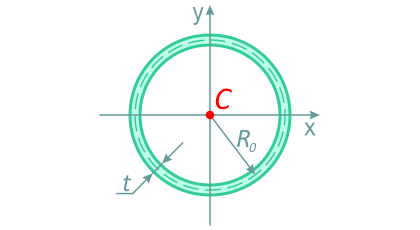
Площадь
![]()
Центральные осевые и полярный моменты инерции трубного сечения
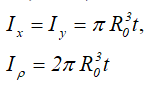
Осевые и полярный моменты сопротивления
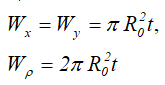
Пример определения координат центра тяжести сложной фигуры:
Далее: