Рассмотрим общий порядок кинематического анализа редукторов:
Среди заданных зубчатых редукторов имеются планетарные, составные и замкнутые дифференциальные механизмы. В планетарных (W=1) и дифференциальных (W=2) передачах оси отдельных колес (сателлитов) являются подвижными.
Для решения задачи необходимо разделить механизмы на части, выделив планетарные и дифференциальные, и для каждой части написать уравнение передаточного отношения, используя соответствующий метод.
При решении планетарных и дифференциальных механизмов применяется метод обращения движения (метод остановки водила) – всем звеньям придается дополнительная угловая скорость (-ωH) в результате чего получается обычный механизм с неподвижными осями колес, так как водило Н будет иметь скорость ωH—ωH=0. Общее передаточное отношение сложного механизма определяется решением полученной системы уравнений.
В задании входным звеном является колесо «а», выходным – звено I, поэтому искомым является передаточное отношение ia1 В рассматриваемом примере (рисунок 12) ось колес 8-8′ является подвижной (8-8′ – сателлиты). Они входят в зацепление с колесами 7 и 9, которые называются центральными.
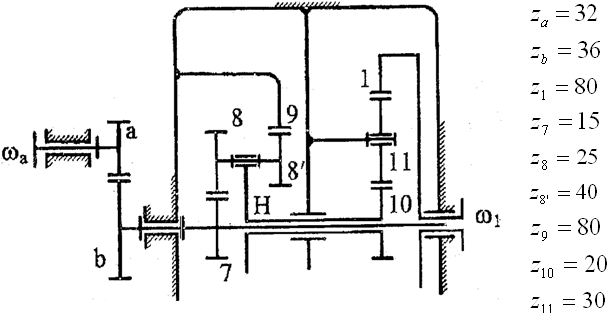
Рисунок 12 — Схема редуктора
Таким образом колеса 7, 8, 8′, 9 и водило Н (звено, соединяющее ось сателлитов с центральной осью) составляют планетарную передачу, а весь механизм делится на три части: – обычная зубчатая пара, 7, 8, 8′, 9 – планетарная часть, 10, 11,1 – обычная (рядовая) передача.
Запишем уравнения для рядовых передач:
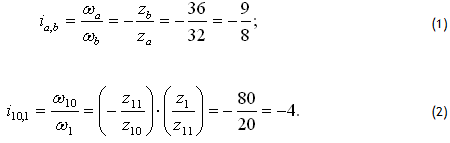
Для планетарной части, после остановки водила “Н”, колеса 7, 8, 8′, 9 будут иметь скорость соответственно: ω7—ωH, ω8—ωH, ω8′—ωH, ω9—ωH а передаточное отношение между центральными колесами
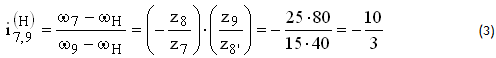
Из (1) ωb=-8/9ωaа из (2) ω10=-4ω1 и с учетом ωb=ω7; ωH=ω10; ω9=0 подставляем в уравнение (3):
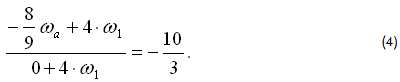
Преобразуем (4), разделив почленно числитель и знаменатель на ω1:
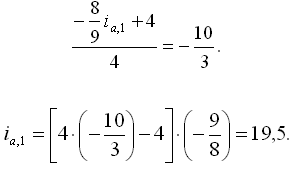
Далее: