Как отмечалось ранее, деформацией при изгибе является искривление продольной оси балки.
Вследствие этого искривления, точки и поперечные сечения балки получают линейные и угловые перемещения.
Рассмотрим на примере простой консольной балки.
Линейные перемещения
Отметим в произвольном месте балки точку K и приложим к свободному концу консоли сосредоточенную силу F.
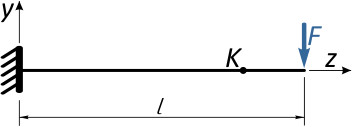
Под действием этой силы балка изогнется, и точка K переместится в новое положение K’.
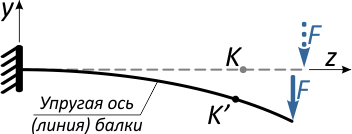
Очевидно, что перемещение точки K произойдет, не строго вертикально, поэтому разложим его на две составляющие:
вертикальное перемещение по оси y, называемое прогибом балки в т. K (yK)
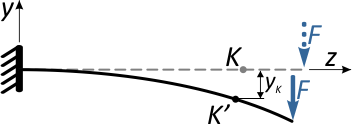
и горизонтальное (осевое) смещение точки вдоль горизонтальной оси — zK
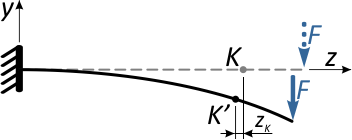
Практические расчеты показывают, что осевые смещения как правило, несоизмеримо меньше вертикальных перемещений (например, в данном случае zK<< yK), поэтому ими пренебрегают, ограничиваясь вычислением прогибов.
Линейные перемещения (прогибы балки) измеряются в метрах или кратных единицах измерения (миллиметрах и сантиметрах).
Прогибы, при которых сечение в результате деформации балки перемещается вверх принимаются положительными.
Именно по величине прогибов определяется жесткость балки.
Угловые перемещения
Кроме линейных, сечения балки при изгибе получают и угловые перемещения.
Проведем касательные к продольной оси балки в точках K и K’.
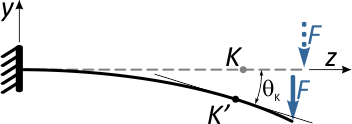
В первом случае линия касательной совпадает с прямой осью балки, во втором – располагается под углом θ.
Угол между касательными очевидно равен углу между нормалями к оси балки в этих точках.
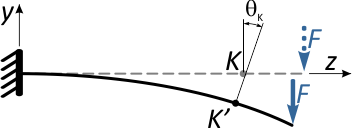
Этот угол θK называется углом наклона сечения K в результате деформации балки.
Вычисляется в радианах, с последующим переводом в градусы.
Между линейными и угловыми перемещениями при изгибе существует дифференциальная зависимость.
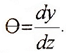
Например, в сечениях, углы наклона которых равны нулю следует ожидать экстремума изогнутой линии балки на данном участке.
Методы расчета перемещений
Существует несколько способов расчета линейных y и угловых θ перемещений при изгибе:
Метод начальных параметров (МНП)
Перемещения рассчитываются по уравнениям МНП
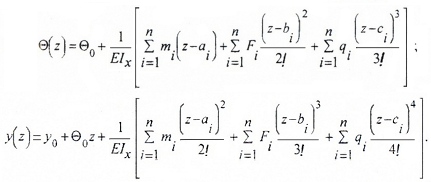
Считается относительно простым методом расчета перемещений в прямых балках с постоянной жесткостью сечения.
Данный способ не применим для расчета прогибов и углов наклона в балках переменного сечения, с изогнутой или ломаной осью и в рамах.
Подробнее >>
Интеграл Мора
Интеграл Мора относится к энергетическим методам расчета перемещений.
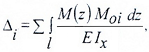
В отличие от МНП позволяет определять линейные и угловые перемещения для любых систем.
Подробнее >>
Способ Верещагина
Данный способ расчета перемещений представляет собой графическую интерпретацию интеграла Мора, особенностью которой является «перемножение эпюр» грузовой и единичных схем.
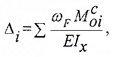
Подробнее >>
Метод интегрирования дифференциального уравнения упругой линии балки
Непосредственное интегрирование дифференциального уравнения упругой линии
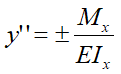
является одним из наиболее универсальных способов расчета перемещений в балках. Может применяться без ограничений к балкам любой формы.
По результатам расчета перемещений сечений балки строится линия изогнутой оси балки (либо эпюра прогибов), с указанием числовых значений прогибов и углов наклона в характерных сечениях.
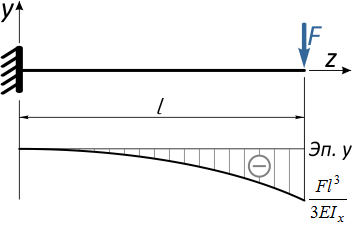
Эти вычисления и построения необходимы для проверки балок на жесткость.
Далее: