Изгибом называется вид деформации бруса, при котором в его поперечных сечениях, под действием внешних нагрузок возникают внутренние изгибающие моменты.
Деформация изгиба проявляется в искривлении продольной оси бруса.
Брус с прямой осью, подвергающийся изгибу, обычно называется балкой.
Если в сечениях балки возникает только изгибающий момент (поперечные силы отсутствуют), то изгиб называется чистым.
При изгибе одни слои балки растягиваются, а противоположные им – сжимаются, например:
Из балки нагруженной только изгибающим моментом
сечениями I и II мысленно вырежем фрагмент длиной dz
Как видно в данном случае верхние слои балки сжаты, а нижние – растянуты.
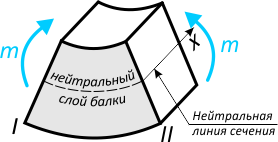
При этом наибольшему растяжению/сжатию подвержены крайние нижний и верхний слои балки.
Между ними расположен нейтральный слой, длина которого вследствие изгиба балки не изменяется.
Нейтральный слой расположен на уровне центров тяжести поперечных сечений балки, нормально к плоскости, в которой действуют изгибающие нагрузки.
Линия, образованная пересечением нейтрального слоя с поперечным сечением балки называется нейтральной линией сечения.
В общем случае плоского прямого изгиба в поперечных сечениях балки возникают два внутренних силовых фактора: изгибающий момент M и поперечная сила Q. Такой изгиб называется поперечным.
Для конкретизации направления внутренних усилий им присваиваются соответствующие индексы:
- Mx — момент, изгибающий относительно оси x (в плоскости yOz);
- Qy — cила, направленная поперек балки вдоль оси y.
Плоский прямой (поперечный) изгиб возникает при действии на балку системы внешних сил, перпендикулярных к ее оси и лежащих в плоскости, проходящей через главную центральную ось сечения балки.
Изогнутая ось балки в этом случае – плоская кривая, совпадающая с плоскостью действия внешних сил.
Для определения внутренних силовых факторов Q и M используется метод сечений, суть которого применительно к балке показана на следующем рисунке:
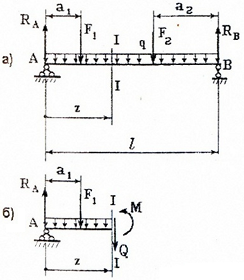
Рассматривая равновесие левой от сечения (I-I) части
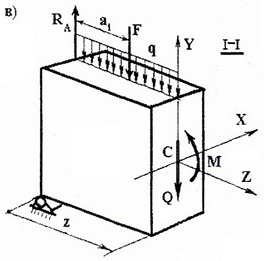
с учетом правила знаков для Q и M, запишем следующие уравнения равновесия:
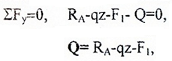
или в общем виде:
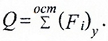
Внутренняя сила Q в поперечном сечении балки численно равна алгебраической сумме проекций на плоскость сечения всех внешних сил (активных и реактивных), действующих по одну сторону от рассматриваемого сечения.
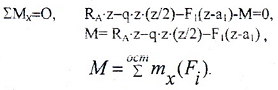
Изгибающий момент в поперечном сечении численно равен алгебраической сумме моментов внешних сил и пар, вычисленных относительно нейтральной оси рассматриваемого сечения и действующих по одну сторону от проведенного сечения.
Между изгибающим моментом M, поперечной силой Q и интенсивностью распределенной нагрузки q существуют следующие дифференциальные зависимости:
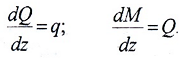
Эти формулы могут быть использованы при построении и проверке эпюр Q и M.
Графические изображения функций Q и M по длине балки называют эпюрами поперечных сил и изгибающих моментов.
Далее: