Пример решения задачи по расчету уравновешивающего внешнего крутящего момента из условия равновесия вала.

Задача

Вал нагружен скручивающими моментами. Определить величину и направление неизвестного уравновешивающего момента M₂ (рис. 1), если M₁=30кНм, M₃=44кНм, M₄=6кНм

Другие примеры решений >
Помощь с решением задач >

Пример решения

Величина и направление неизвестного скручивающего момента M₂ определяется из условия неподвижности вала.

Конечно на самом деле вал при работе вращается, собственно для этого он и предназназначен — вращаясь передавать крутящий момент.

Но в сопротивлении материалов, при расчетах валов, часть крутящего момента необходимая для вращения вала отбрасывается, и учитываются только моменты деформирующие (скручивающие) вал.

Таким образом будем полагать что рассматриваемый вал не вращается. Для этого должно выполняться следующее условие: сумма крутящих моментов относительно продольной оси вала должна быть равна нулю

Для составления уравнения равновесия зададим произвольным образом направление искомого крутящего момента M₂, например по ходу часовой стрелки (рис. 2)

Запишем уравнение равновесия вала относительно продольной оси z, при этом моменты вращающие вал в одну сторону запишем со знаком «+», а моменты обратного направления соответственно со знаком «-«:

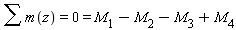
отсюда следует, что

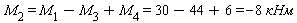
Знак «-» в результате показывает, что реальное направление крутящего момента M₂ противоположно ранее выбранному, т.е. в данном случае момент M₂ направлен против хода часовой стрелки и равен 8кНм.

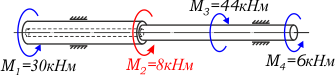
Проверить себя можно сложив отдельно величины крутящих моментов направленных по ходу часовой стрелки и моментов обратного направления. Эти суммы должны получиться одинаковыми.

Другие примеры решения задач >