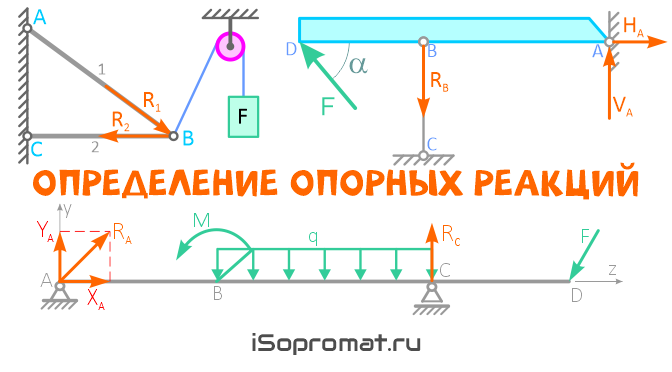
Определением реакций опор называют расчет величины и направления реактивных (т.е. ответных) сил и моментов, возникающих в опорах конструкций под действием системы заданных внешних нагрузок.
В рассмотренных ниже примерах, для наглядности, заданные внешние нагрузки показаны синим или зеленым цветом, а реакции опор — красным или оранжевым.
При решении задач, определяемые реакции опор могут обозначаться по-разному:
- буквой R (от англ. Reaction). В этом случае, для уточнения точки приложения и направления силы могут добавляться соответствующие индексы (например, RAy — это реакция в точке A направленная вдоль оси Y);
- буквами V (Vertical) и H (Horizontal) обозначаются соответственно вертикальная и горизонтальная составляющие полной реакции (например, HB — это реакция в точке B направленная вдоль оси балки);
- Также возможно обозначение реакций по осям координат — YA, XB и т.д.
Рассмотрим решение всех типов задач по расчету величины и направления опорных реакций в заделках, шарнирных опорах и стержнях балочных систем.
Примеры определения опорных реакций
Примеры нахождения реакций опор для различных способов закрепления и нагружения бруса, балок, балочных систем, рам и других элементов конструкций.
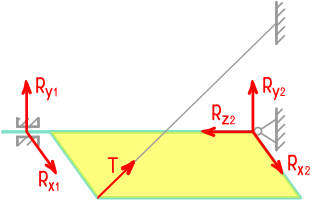
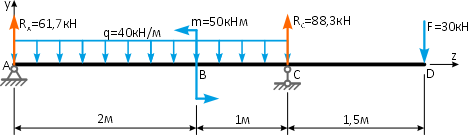
Реакции опоры и стержня системы
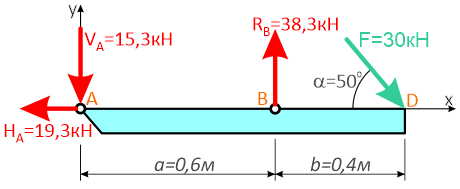
Невесомая балка удерживается в горизонтальном положении шарнирно-неподвижной опорой в т. A и вертикальным стержнем BC.
В точке D к балке приложена сосредоточенная сила F=30кН под углом 50°.
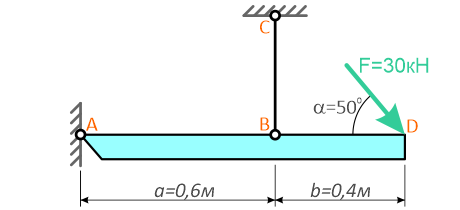
Требуется найти реакции, возникающие в опоре A и стержне BC.
Решение
Для решения задачи, покажем систему координат x-y и зададим произвольное направление реакций.
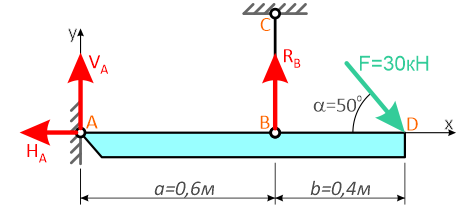
В точке A реакция в опоре раскладывается на две составляющие — вертикальную VA и горизонтальную HA.
Реакция в стержне (RB) всегда направлена вдоль самого стержня.
Для определения трех реакций требуется составить три уравнения равновесия.
Это будут два уравнения суммы моментов относительно точек в опорах и сумма проекций всех сил на ось x равные нулю.
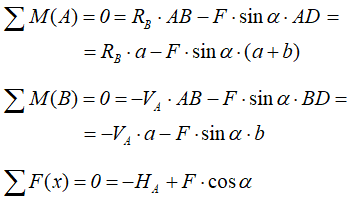
Из полученных уравнений выражаем и находим искомые реакции опор
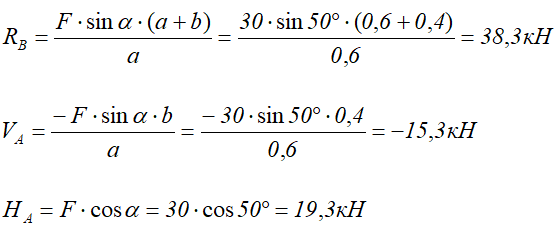
Вертикальная реакция в опоре A получилась отрицательной, это значит что она направлена в противоположную сторону.
Направляем ее вниз, изменив знак на «плюс».
Выполним проверку найденных реакций, проецируя все силы на ось y.
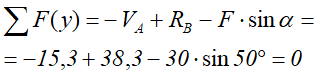
Равенство нулю суммы проекций всех сил и реакций указывает на то, что реакции опор найдены верно.
Таким образом, заданная балка удерживается в равновесии под действием одной активной и трех реактивных сил.
Расчет реакций в опорах балочных систем
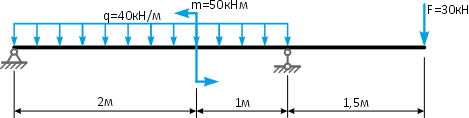
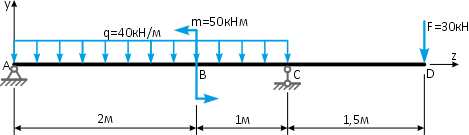
Простая балочная система на двух шарнирных опорах находится под действием внешней нагрузки, включающей силу F=60кН, приложенную под углом 40°, момент M=45кНм и равномерно распределенную нагрузку q=18кН/м.
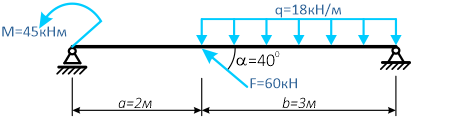
Требуется определить реакции в опорах A и C.
Решение
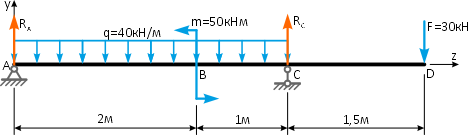
Вычерчиваем заданную схему в масштабе, показываем численные значения нагрузок, систему координат x-y и задаем произвольное направление реакций.
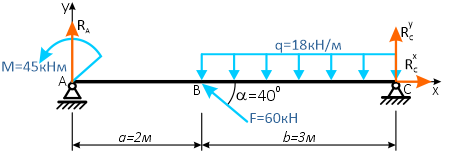
Здесь, в шарнирно-подвижной опоре будет только одна составляющая реакции.
Для упрощения решения, распределенную нагрузку можно заменить её равнодействующей, которая при равномерной интенсивности нагрузки q будет приложена по её центру
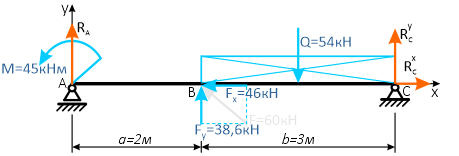
и будет иметь величину
![]()
Силу F можно разложить на составляющие, спроецировав её на оси x и y.
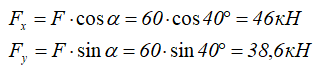
Аналогично тому, как это делалось при решении предыдущей задачи, записываем уравнения равновесия балки: нулевые суммы моментов всех нагрузок и искомых реакций относительно опор
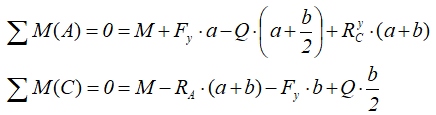
и проекций сил на ось балки
![]()
Откуда находим все три опорные реакции
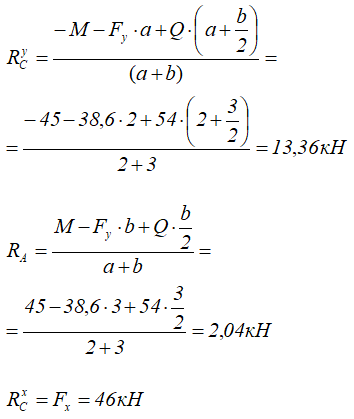
Значения реакций положительны, следовательно, направление реакций было выбрано верно.
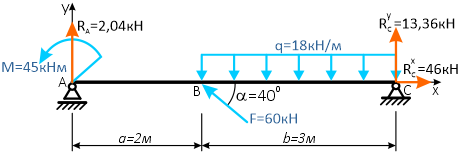
Проверяем найденные значения.
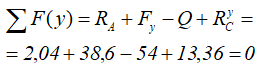
Величина и направления реакций определены правильно.
Подробное решение данного типа задач
Другие типы задач по определению опорных реакций с детальным разбором выполняемых действий:
Определение опорных реакций систем
Расчет реакций в опорах плоских и пространственных систем.
Другие примеры решения задач равновесия
Реакции опор при растяжении и сжатии стержней
Определение реакций в опорах стержней и стержневых систем при действии продольных сосредоточенных сил и распределенных нагрузок.
Реакции при кручении валов
Примеры расчета опорных моментов и реакций в подшипниках вала при кручении.
Опорные реакции при изгибе балок и рам
Определение реакций в шарнирных опорах и заделках консольных балок и рам при действии систем внешних сил, моментов и распределенных нагрузок.
Наш короткий видеоурок по расчету реакций опор балки:
Типы опор и их реакции
В механике различают тела свободные: возможность перемещения, которых в любом направлении ничем не ограничена, и несвободные, когда перемещение данного тела ограничивают другие тела.
Сами тела ограничивающие свободу перемещения данного тела называют опорами (связями), а силы, с которыми опоры удерживают данное тело в равновесии, называют реакциями опор.
Направление реакций зависит от вида опор и схемы нагружения.
При решении задач очень важно правильно заменить опоры их реакциями, иначе записанные уравнения равновесия окажутся неверными.
И здесь важно помнить о том, что реакции могут появляться только по тем направлениям, в которых перемещение невозможно.
Рассмотрим определение реакций в основных типах опор:
Реакция гладкой поверхности
Пусть некоторое тело опирается на гладкую поверхность.
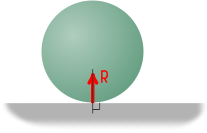
Здесь перемещение тела возможно только вдоль поверхности.
Движение перпендикулярно ей исключено.
Потому что перемещению в сторону поверхности препятствует сама поверхность, а при движении от нее нарушится сама связь.
Таким образом, гладкая поверхность препятствует перемещению тела только в направлении нормали, поэтому реакция гладкой поверхности всегда направлена по нормали к этой поверхности.
При взаимодействии криволинейных поверхностей аналогично, реакция направлена нормально к касательной в точке контакта тел.
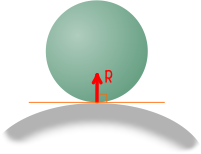
Такое же направление имеет место при контакте в двух точках.
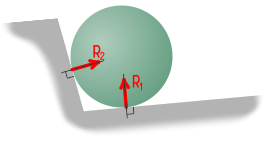
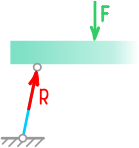
Реакция ребра
В случае, когда прямая балка опирается на ребро, реакции будут направлены перпендикулярно опираемой или опирающейся плоскости в точке их касания.
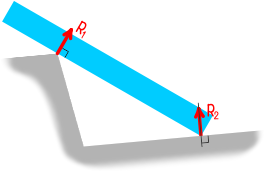
При повороте балки реакция всегда будет оставаться нормальной к соответствующей поверхности.
Гибкая связь
Для тела, подвешенного на нерастяжимой нити или тросе, связь не позволяет телу удаляться от точки подвеса в направлении самой нити.
Поэтому реакция гибкий связи будет направлена всегда только вдоль самой нити.
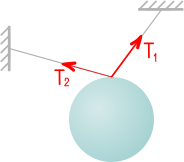
Реакции в стержнях
Как и в предыдущем пункте, в стержнях, которые с помощью шарниров соединяют какие-либо элементы с опорами, реакции направлены вдоль самих стержней.
Но в отличие от нитей, здесь может быть одно из двух направлений: растягивающее стержень или сжимающее его.
Реакции в шарнирных опорах
В плоскости возможны только три направления перемещения: линейные — вдоль осей x и y, и вращение относительно оси Z.
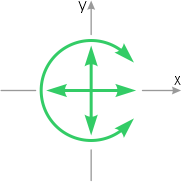
Реакции в опорах возникают по направлениям, в которых опоры ограничивают перемещение.
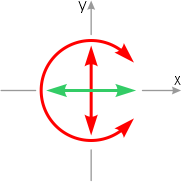
Поэтому в двумерных системах каждая опора может давать не более трех реакций.
Если свободное тело закрепить шарнирно-неподвижной опорой, которая допускает вращение, но исключает любые линейные перемещения, то в такой опоре могут возникать две реакции.
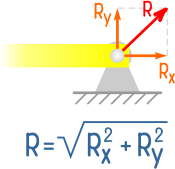
Они являются осевыми проекциями полной реакции опоры, которая может быть найдена как корень из суммы квадратов её составляющих.
Направление вектора полной реакции зависит от схемы нагружения элемента.
Встречаются разные способы изображения шарнирно-неподвижных опор в расчетных схемах.
В шарнирно-подвижных опорах, помимо вращения возможно линейное перемещение вдоль поверхности, поэтому здесь будет только одна, нормальная к поверхности, составляющая реакции, которая по направлению и величине будет совпадать с полной.
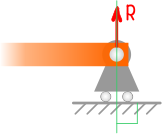
У таких опор так же существуют дополнительные варианты схематичного изображения.
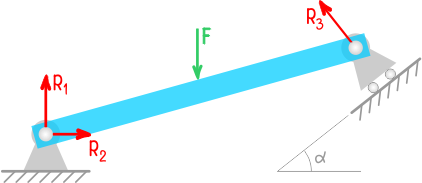
Пример направления реакций опор для балки на двух шарнирных опорах.
Реакции в заделках
Вид связи, при котором брус жестко закреплен в опоре называется глухой заделкой.
В этом случае исключены любые перемещения элемента.
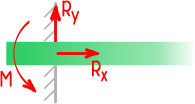
Поэтому в плоских заделках может возникать до трех реакций: горизонтальная и вертикальная составляющие полной реакции, а также момент.
Скользящая заделка допускает линейное перемещение вдоль одной из осей.
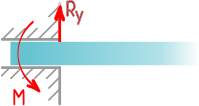
Следовательно, по этой оси реакции не будет.
В бискользящей заделке исключается только угловое перемещение элемента.
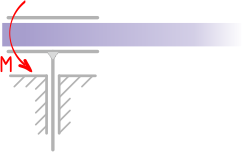
Здесь из реакций будет один момент.
Реакции опор в трехмерных системах
В пространстве возможно уже шесть направлений движения:
Поступательные вдоль каждой из осей и вращение относительно них.
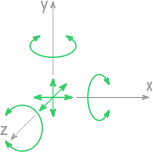
Поэтому в трехмерных системах опоры могут давать до шести реакций.
Шкив на валу, закрепленном подшипниками, может вращаться относительно продольной оси вала.
Любые другие перемещения невозможны.
В силу конструктивных особенностей подшипников моментов в них не возникает.
Здесь имеют место только реактивные силы.
В радиальном подшипнике (который справа) все реакции поперечны оси вала.
В радиально-упорном (который слева) добавляется еще и продольная.
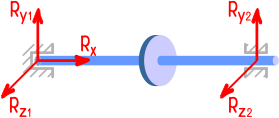
В трехмерном шарнире исключены любые линейные перемещения и возможны только повороты относительно трех осей, что дает до трех составляющих полной реакции R.
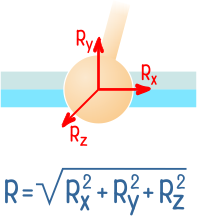
В жесткой заделке при общем случае нагружения может возникать до шести реакций: трёх сил и трех моментов.
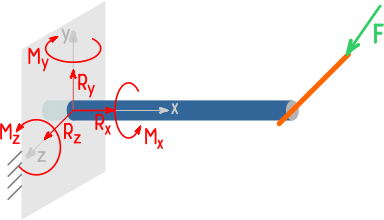
Пример замены опор их реакциями для трехмерной системы:
Порядок определения опорных реакций
В рассмотренных выше примерах при определении реакций в опорах выполняется следующая последовательность действий:
- Вычерчивается (в масштабе) расчетная схема элемента с указанием всех размеров и приложенных внешних нагрузок
- Выбирается система координат, и обозначаются характерные сечения бруса
- Определяется количество и возможное направление связей
- Записываются уравнения статики (по количеству неизвестных реакций)
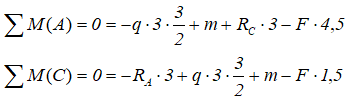
- Из уравнений равновесия находим величину и направление (по знаку) опорных реакций
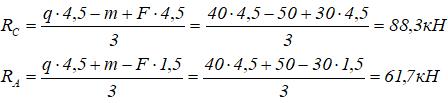
После расчетов выполняется проверка найденных значений.
Более подробно порядок расчета опорных реакций рассматривается в разделе «Статика» теоретической механики.
Далее: