Рассмотрим три существующих способа задания движения материальной точки: координатный, векторный и естественный.
Чтобы иметь возможность определить параметры движения точки необходимо задать закон ее движения.
В зависимости от известных величин и поставленной задачи могут быть использованы следующие способы задания движения точки: векторный, координатный и естественный.
Векторный способ
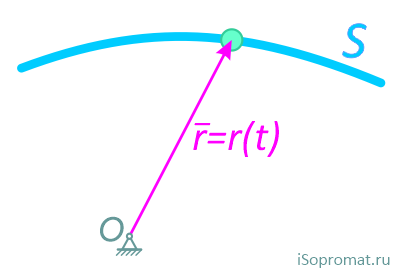
При векторном способе задания движения положение точки определяется радиус-вектором, проведенным из неподвижной точки в выбранной системе отсчета.
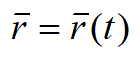
Координатный способ
При координатном способе задания движения задаются координаты точки как функции времени:
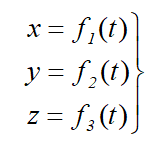
Это параметрические уравнения траектории движущейся точки, в которых роль параметра играет время t.
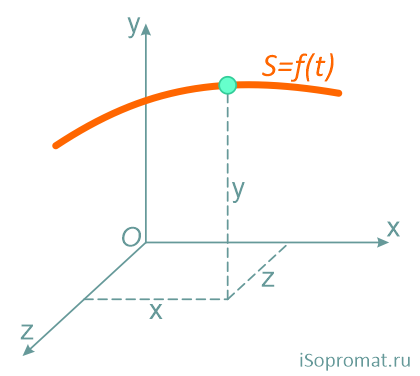
Чтобы записать уравнение траектории движения материальной точки в явной форме, надо исключить из них параметр времени t.
Естественный способ
При естественном способе задания движения задаются траектория точки, начало отсчета на траектории с указанием положительного направления отсчета, закон изменения дуговой координаты: s=s(t).
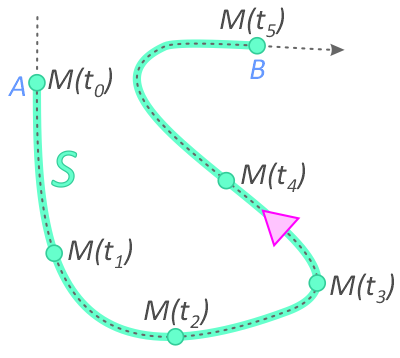
Этим способом удобно пользоваться, если траектория точки заранее известна.
Примеры решения задач >
Далее: Скорость точки