При плоском движении ускорения точек твердого тела определяются согласно следующей теореме:
Из выражения
![]()
или
![]()
путем дифференцирования получаем
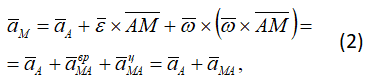
где
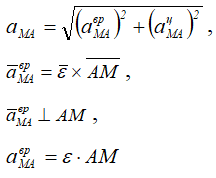
— вращательное ускорение точки М при вращении вокруг точки А.
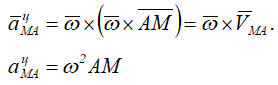
— центростремительное ускорение точки М при вращении вокруг точки А.
Центростремительное ускорение aцMA направлено от точки М к полюсу А.
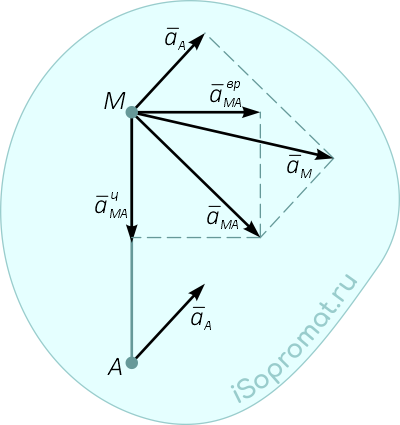
Рисунок 1
Численную величину полного ускорения можно определить, спроецировав векторное равенство (2) на выбранные оси координат:
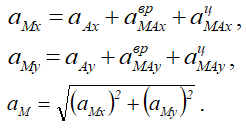
Далее: