Определение координат центра тяжести x_C и y_C плоских фигур сложной формы выполняется при решении задач для последующих расчетов других геометрических характеристик, например, таких как радиусы инерции и моменты инерции поперечных сечений.

Рассмотрим способы и пример определения координат положения центра тяжести фигуры нестандартной формы.

Способы определения координат центра тяжести

Способы определения координат центров тяжести твердых объёмных тел и плоских фигур можно получить исходя из полученных ранее общих формул для расчета положения центра тяжести.

Существует 5 способов расчета координат положения центра тяжести сложных тел и фигур:

1. Аналитический (путем интегрирования).
2. Метод симметрии. Если тело имеет плоскость, ось или центр симметрии, то его центр тяжести лежит соответственно в плоскости симметрии, оси симметрии или в центре симметрии.
3. Экспериментальный. (метод подвешивания тела).
   Этот способ подходит в основном для плоских и линейных тел.
4. Разбиение. Тело или фигура разбивается на конечное число частей (простых тел или фигур), для каждой из которых положение центра тяжести C и площадь A известны.
   Например, проекцию тела на плоскость xOy (рисунок 1.8) можно представить в виде двух плоских фигур с площадями A₁ и A₂ (A = A₁+ A₂).
   
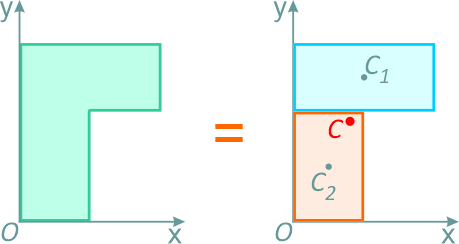   Рисунок 1.8

   Центры тяжести этих фигур находятся в точках C₁(x₁, y₁) и C₂(x₂, y₂). Тогда координаты центра тяжести тела равны:
   

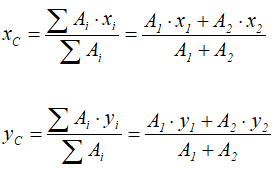
5. Дополнение (Метод отрицательных площадей или объемов).
   Это частный случай предыдущего способа разбиения. Он применяется к телам, имеющим вырезы, если центры тяжести тела без выреза и вырезанной части известны.
   Например, необходимо найти координаты центра тяжести плоской фигуры (рисунок 1.9):
   
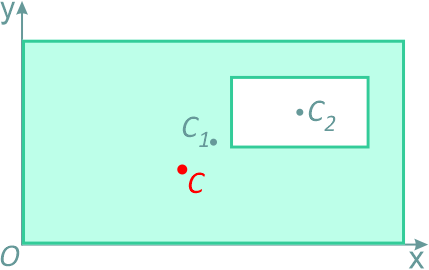   Рисунок 1.9

   Тогда координаты центра тяжести фигуры с отверстием можно определить по формулам:
   

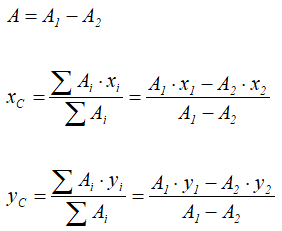
При решении задач по определению координат центра тяжести плоских фигур и объемных тел применяются последние два способа (разбиение и дополнение).

Пример определения координат центра тяжести сложной фигуры в нашем коротком видео:

Другие видео

Пример определения координат центра тяжести плоской фигуры

Задача

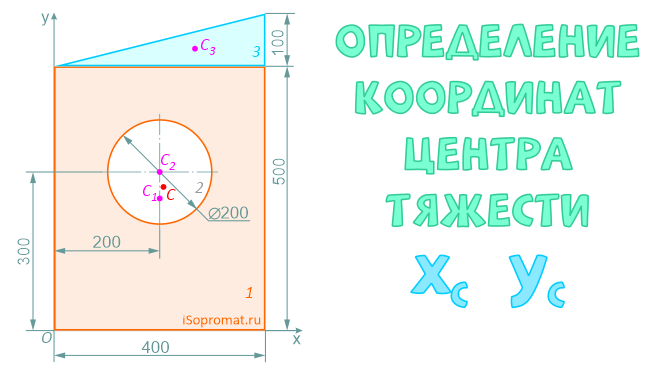
Определить координаты центра тяжести плоской фигуры с круглым отверстием

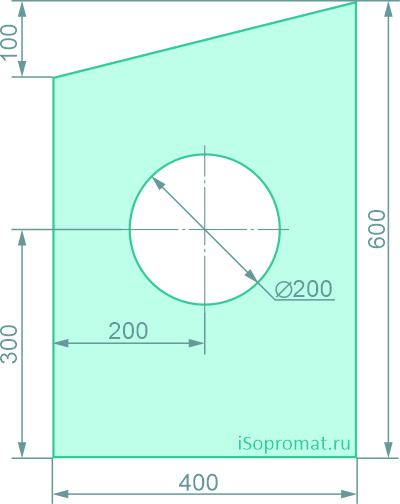
Решение

Через нижнюю левую точку фигуры проведем координатные оси x и y.

Разделим заданное сечение на простые фигуры – прямоугольник, круг и прямоугольный треугольник.

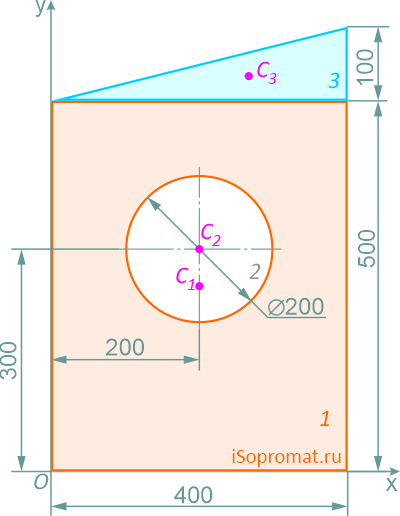
Рассчитаем необходимые для решения задачи площади A и координаты x, y центров тяжести C_i отдельных фигур:

Прямоугольник (фигура 1)
Площадь
A₁ = 400×500=200000 мм²
Положение центра тяжести
x₁ = 200 мм
y₁ = 250 мм

Круг (2) (вычитаемая фигура)
Площадь
A₂ = π×200²/4 = 31416 мм²
Координаты центра тяжести круга:
x₂ = 200 мм
y₂ = 300 мм

Прямоугольный треугольник (3)
Площадь
A₃ = 400×100/2 = 20000 мм²
Положение центра тяжести треугольника находится на пересечении его медиан (на расстоянии 1/3 высоты от основания или 2/3 высоты от его вершин)
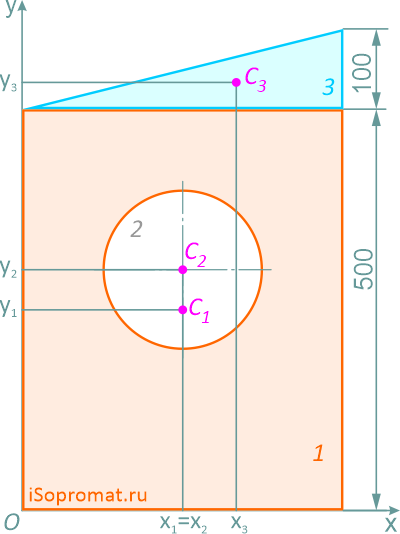
x₃ = 400×2/3 = 266,7 мм
y₃ = 500+100×1/3 = 533,3 мм

Координаты x и y центра тяжести C всей плоской фигуры определим по формулам:

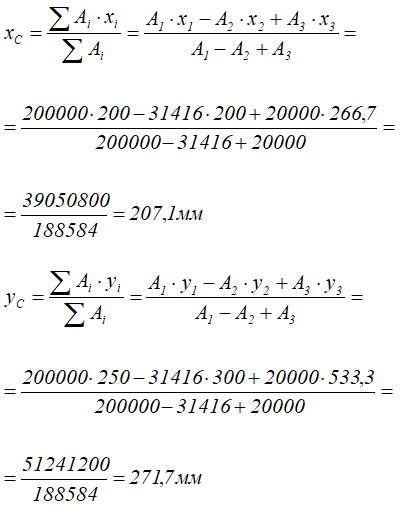
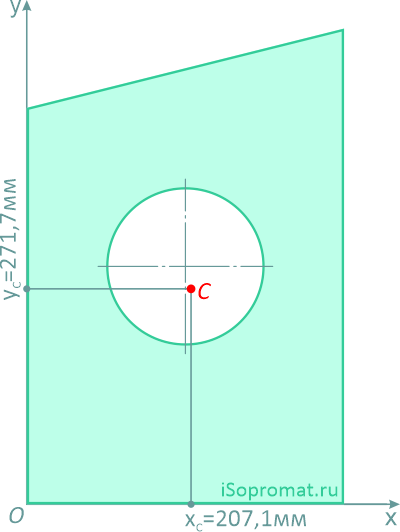
Ответ: Таким образом, центр тяжести заданной фигуры находится в точке C с координатами x_C = 207,1 мм, y_C = 271,7 мм.

---

Далее: