Рассмотрим связь момента силы относительно оси и момента относительно точки:
Проведем через точку O, где задан момент силы относительно точки MO(F) декартовы оси координат x, y, z (рисунок 14).
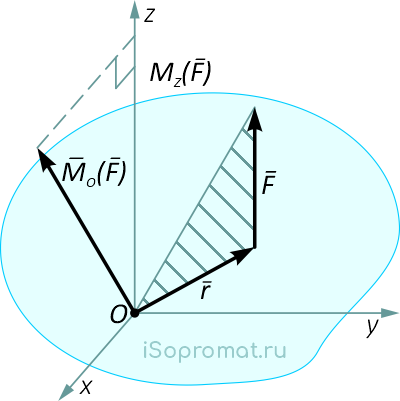
Рисунок 14
Момент силы относительно точки можно представить в виде суммы трех векторов
![]()
Наш короткий видеоурок про момент силы с примерами:
Эти вектора являются моментами силы относительно осей x, y, z:
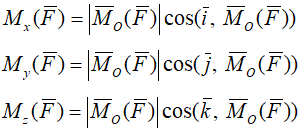
Момент силы относительно оси равен проекции на эту ось момента силы относительно любой точки на оси.
Далее: