Угловой скоростью при сферическом движении называют векторную величину, характеризующую быстроту вращения твердого тела вокруг точки, определяемую как приращение угла поворота тела за промежуток времени.

Рассмотрим бесконечно малый промежуток времени Δt → 0, за который твердое тело совершает поворот на бесконечно малый угол Δα вокруг мгновенной оси Ω (рисунок 1).

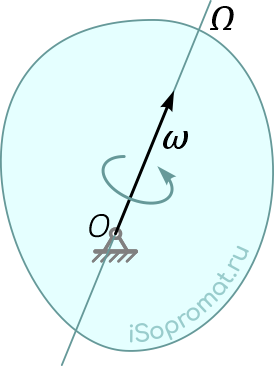
Рисунок 1

Предел отношения

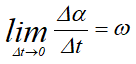
называется угловой скоростью при сферическом движении твердого тела в рассматриваемый момент времени

Угловая скорость является векторной величиной. Вектор угловой скорости ω может быть приложен к любой точке мгновенной оси и направлен в каждый момент времени по мгновенной оси Ω, так, чтобы смотря навстречу этому вектору, видеть вращение тела происходящим против движения часовой стрелки.

Угловым ускорением при сферическом движении называют степень изменения угловой скорости.

За вектор углового ускорения ε при вращении тела вокруг неподвижной точки принимают вектор, который характеризует изменение угловой скорости ω в данный момент как по числовой величине, так и по направлению.

Такой характеристикой является производная по времени от вектора угловой скорости ω.

Таким образом, угловое ускорение при сферическом движении определяется так:

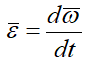
В общем случае угловое ускорение не направлено по мгновенной оси, а, как производная по времени от вектора ω, параллельно касательной к годографу этого вектора.

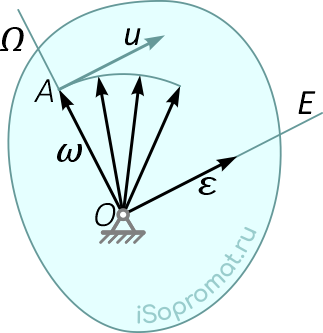
Рисунок 2

Условимся угловое ускорение ε изображать в любой точке прямой, параллельной этой касательной годографа угловой скорости u, но проходящей через неподвижную точку тела (рисунок 2).

Прямая, по которой направлен вектор углового ускорения, называется осью углового ускорения и обозначается E.

Далее: