Вращательное движение твердого тела – это движение, при котором тело имеет как минимум две неподвижные точки (рисунок 13).
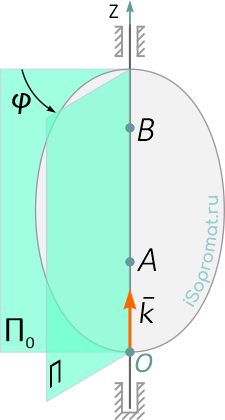
Рисунок 13
Прямая, проходящая через эти точки, называется осью вращения.
Положение тела определено, если задан угол φ между плоскостями П0 и П, одна из которых неподвижна, а другая жестко связана с телом.
Уравнение вращательного движения твердого тела.
![]()
За положительное направление отсчета принимается вращение против хода часовой стрелки, если смотреть навстречу положительному направлению оси z.
Траекториями точек тела при его вращении вокруг неподвижной оси являются окружности, расположенные в плоскостях, перпендикулярных оси вращения.
Характеристики вращательного движения
Для характеристики изменения угла поворота с течением времени вводится величина, называемая угловой скоростью ω:
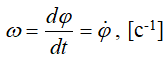
В технике угловая скорость – это частота вращения, выраженная в оборотах в минуту. За одну минуту тело повернется на угол 2πn, где n – число оборотов в минуту (об/мин). Разделив этот угол на число секунд в минуте, получим
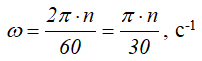
Вектор угловой скорости – это вектор, направленный по оси вращения в ту сторону, откуда вращение видно происходящим против хода часовой стрелки, с модулем, равным модулю алгебраической угловой скорости
![]()
где k – единичный вектор оси вращения.
Угловое ускорение – мера изменения угловой скорости:
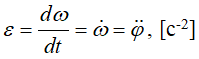
Вектор углового ускорения – производная вектора угловой скорости по времени (рисунок 1.4)
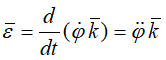
Если ε > 0 и ω > 0 (рисунок 14), то угловая скорость возрастает с течением времени и, следовательно, тело вращается ускоренно в рассматриваемый момент времени в положительную сторону. Направление векторов ω и ε совпадают, оба они направлены в положительную сторону оси вращения Oz.
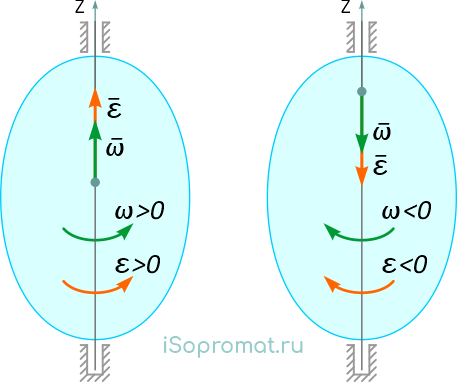
Рисунок 14
При ε < 0 и ω < 0 – тело вращается ускоренно в отрицательную сторону. Направление векторов ω и ε совпадают, оба они направлены в отрицательную сторону оси вращения Oz.
Если ε < 0 и ω > 0, то имеем замедленное вращение в положительную сторону. Векторы ω и ε направлены в противоположные стороны.
Если ε > 0 при ω < 0 (рисунок 15), то имеем замедленное вращение в отрицательную сторону. Векторы ω и ε направлены в противоположные стороны.
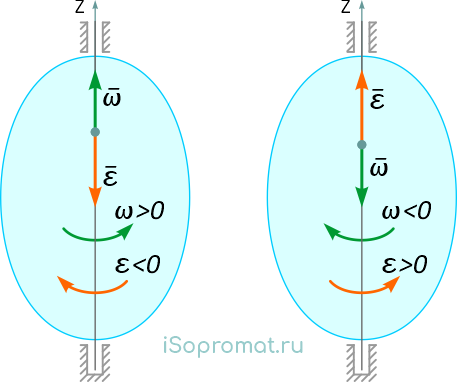
Рисунок 15
Если угловая скорость ω = const, то вращательное движение называется равномерным. Уравнение равномерного вращения
![]()
Если угловое ускорение ε = const, то вращательное движение называется равнопеременным.
Уравнение равнопеременного вращения
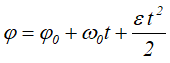
и уравнение, выражающее угловую скорость в любой момент времени
![]()
представляют совокупность основных формул вращательного равнопеременного движения тела.
Далее: