Аксиомы статики — принимаемые без доказательств положения технической и теоретической механики, на основании которых выводятся условия равновесия систем сил для определения неизвестных усилий.
Аксиомы статики твердого тела обобщают многовековой опыт наблюдения физических явлений.
Аксиомы 1 и 5 представляют собой общие законы классической механики Галилея и Ньютона.
Аксиомы 2, 3 и 4 могут быть выведены из общих законов механики как следствие.
Первая аксиома статики. Закон инерции
Аксимома инерции: «Изолированная от действия других тел материальная точка под действием уравновешенной системы сил находится в покое или движется равномерно и прямолинейно».
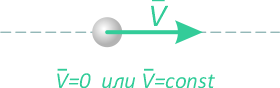
Равномерное и прямолинейное движение материальной точки называется движением по инерции.
Из первой аксиомы следует, что покой и движение по инерции являются эквивалентными механическими состояниями материальной точки.
Это относится и к твердому телу, однако для него кроме поступательного равномерного прямолинейного существуют и другие виды движения по инерции.
Если же материальная точка или твердое тело находится в покое или движется по инерции под действием некоторой системы сил, то такая система сил называется уравновешивающейся.
Аксиома о равновесии двух сил
Вторая аксиома статики гласит: «Абсолютно твердое тело находится в равновесии под действием двух сил тогда и только тогда, когда эти силы равны по модулю, действуют по одной прямой и направлены в противоположные стороны».
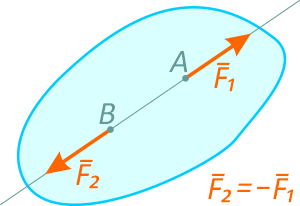
Таким образом, для равновесия двух сил приложенных к твердому телу необходимо и достаточно чтобы они были равны по модулю и направлены по одной прямой в противоположные стороны.
Данная аксиома определяет простейшую уравновешивающуюся систему сил приложенных к твердому телу, силы равны по модулю и направлены в противоположные стороны, т.е. F2=-F1.
Надо отметить, что силы должны быть направлены вдоль одной линии действия.
Аксиома о присоединении и исключении уравновешивающихся сил
Согласно третьей аксиоме, не нарушая состояния абсолютно твердого тела, к нему можно прикладывать или отбрасывать от него уравновешенную систему сил.
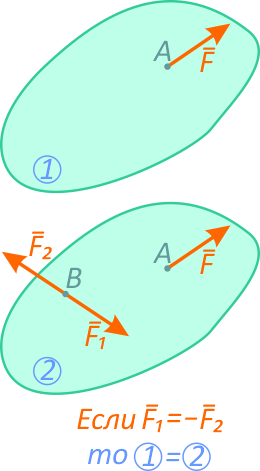
Другими словами, действие системы сил на твердое тело не изменится, если прибавить к ней или отнять от нее уравновешивающуюся систему сил.
Следствие из третьей аксиомы: не изменяя действие силы на твердое тело точку приложения силы можно переносить по линии её действия.
Предположим, что к твердому телу в точке A приложена сила F.
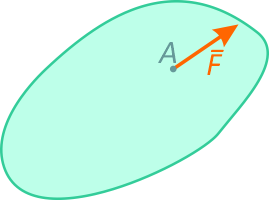
Докажем что действие силы на твердое тело не изменится если точку приложения силы перенести по линии ее действия.
Покажем линию действия силы F и выберем на линии действия этой силы произвольную точку B.
Приложим в точке B две взаимно уравновешивающиеся силы F1 и F2 равные по модулю силе F и направленные по прямой AB. При этом F1=F=-F2.
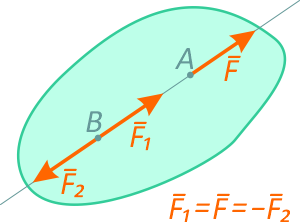
Согласно аксиоме №3 система трех сил F, F1 и F2 эквивалентна силе F.
Но силы F и F2 равны по модулю и направлены по одной прямой в противоположные стороны.
На основании той же аксиомы 3 их можно отбросить как взаимно уравновешивающиеся.
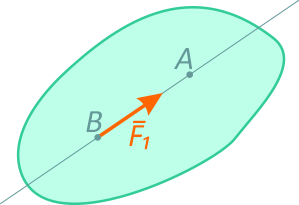
В результате на твердое тело будет действовать одна сила F1 равная силе F и эквивалентная ей, но приложенная в точке B.
Таким образом, в статике твердого тела силу можно рассматривать как скользящий вектор, определяемый модулем, линией действия и направлением.
Данное следствие применимо только для сил, действующих на абсолютно твердое тело.
В инженерных расчетах им можно пользоваться лишь тогда, когда определяются условия равновесия какой-либо жесткой конструкции и не рассматриваются возникающие в ней внутренние напряжения и деформации.
Аксиома 4. Правило параллелограмма сип
По четветрой аксиоме статики, две силы, приложенные к телу в одной точке, имеют равнодействующую, проходящую через эту точку и равную их геометрической сумме.
Равнодействующая двух сил, приложенных к телу в одной точке, изображается диагональю параллелограмма построенного на этих силах.
Пусть к твердому телу в точке A приложены силы F1 и F2.
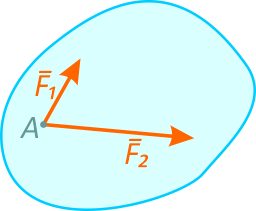
Построим параллелограмм сил и определим их действующую, обозначаемую буквой R.
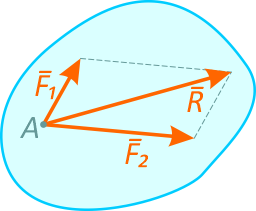
Построение параллелограмма можно заменить построением треугольника сил:
Из точки A откладываем вектор F1 от стрелки которого отложим вектор F2.
Вектор равнодействующей R получим, соединив начало вектора F1 с концом вектора F2.
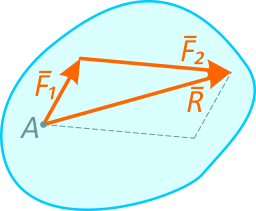
Аксиому 4 можно сформулировать иначе: равнодействующая двух сил, приложенных к телу в одной точке, равна геометрической сумме этих сил и приложена в той же точке.
Правила параллелограмма и треугольника можно обобщить на систему сил приложенных в одной точке.
Применяя последовательно правило треугольника можно построить многоугольник нескольких сил, равнодействующая которого является замыкающий стороной многоугольника сил.
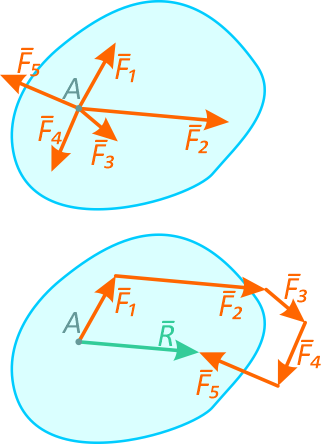
Таким образом, равнодействующая системы сходящихся сил равна их геометрической сумме и приложена в той же точке.
Аксиома №5. Закон равенства действия и противодействия сил.
Пятая аксиома статики гласит: «Силы взаимодействия двух тел равны по модулю и направлены по одной прямой в противоположные стороны».
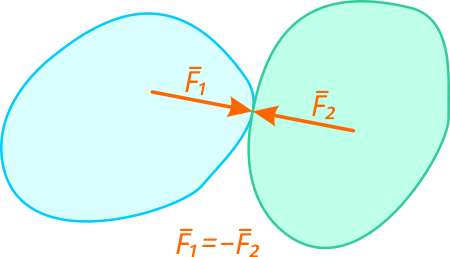
Силы, с которыми два тела действуют друг на друга, всегда равны по модулю и направлены по одной прямой в противоположные стороны.
Отметим, что силы действия и противодействия не уравновешиваются, так как приложены к разным телам.
Аксиома 6. Принцип отвердевания
Аксиома о сохранении равновесия сил, приложенных к деформируемому телу, говорит о том, что равновесие деформируемого тела не нарушится, если это тело отвердеет.
Если деформируемое тело под действием данной системы сил находится в равновесии, то оно сохранит состояние равновесия и после его отвердевания.
Из этой аксиомы вытекает, что условия равновесия твердого тела должны соблюдаться и для деформируемых тел.
Однако, условия равновесия необходимые и достаточные для абсолютно твердого тела могут быть недостаточными для тела деформируемого.
Приведем простой пример: для равновесия твердого стержня под действием двух сил приложенных к его концам необходимо и достаточно чтобы эти силы были равны по модулю и направлены вдоль стержня в противоположные стороны.
А для упругой нити эти условия необходимы но недостаточны, т.к. нить будет находиться в равновесии при наличии дополнительного условия: силы, действующие на нее должны быть растягивающими, но не сжимающими.
Принцип отвердевания позволяет применять уравнение равновесия твердого тела к деформируемым телам.
Этим объясняется широкое применение уравнений статики твердого тела в теории упругости, сопротивлении материалов, строительной механике и других механических дисциплинах, следующих за технической и теоретической механикой.
Далее: