Решения задач по разделу «Статика» теоретической, технической и инженерной механики.

Определение реакций стержней под действием груза

Задача

Стержневая система из двух стержней AB и BC соединенных между собой и закрепленных в опоре шарнирно, удерживает на нерастяжимой нити груз весом F = 40 кН.

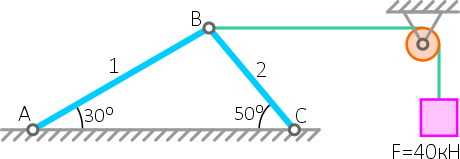
Углы наклона стержня 1 — 30°, стержня 2 — 50°.

Требуется определить величину и направление реакций стержней, под действием груза.

Решение задачи

Все элементы заданной системы неподвижны, т.е. находятся в состоянии статического равновесия.

Рассмотрим равновесие шарнира В.

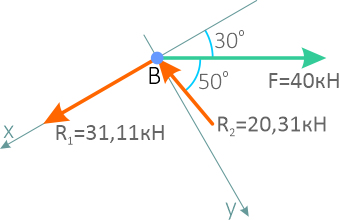
Для этого освобождаем шарнир B от связей и изображаем действующие на него вдоль стержней 1 и 2 и нити удерживающей груз F активные силы и реакции связей.

Выбираем положение системы координат X-Y. Начало координат совмещаем с точкой В.
Ось Х совместим с направлением линии действия одной из неизвестных реакций, например R₁, а ось Y направим перпендикулярно оси X и определим углы между усилиями и осями.

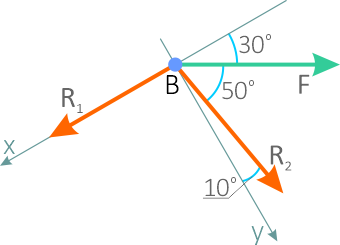
Составляем уравнения равновесия для системы сил, действующих на шарнир В.

Для равновесия точки B, обе суммы проекций всех сил на оси X и Y должны быть равны нулю.

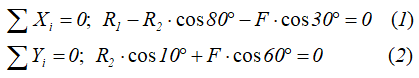
Определяем реакции стержней R₁ и R₂, решая полученную систему уравнений.

Из уравнения (2) определяем величину R₂:

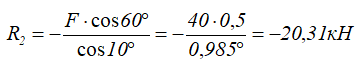
Затем подставляем полученное значение R₂ в уравнение (1) и находим R₁:

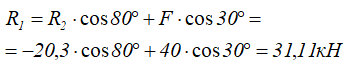
Знак минус перед значением R₂ указывает на то, что первоначально выбранное направление реакции неверное – следует изменить направление реакции R₂ в противоположную сторону, то есть к шарниру В.

Проверка решения графическим способом

Выполним графическую проверку значений найденных реакций с помощью построения силового многоугольника.

Для этого, задав определенный масштаб, переносим силу и реакции опор в заданном положении (сохраняя величину и угол наклона вектора усилий).

При этом каждый следующий вектор откладываем от стрелки предыдущего. Последовательность векторов значения не имеет.

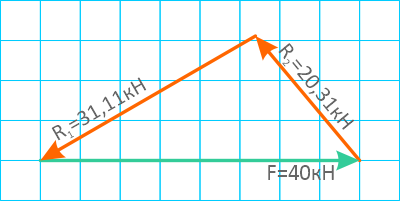
Стрелка последнего вектора совпала с началом первого. Следовательно, величина и направление реакций были определены правильно.

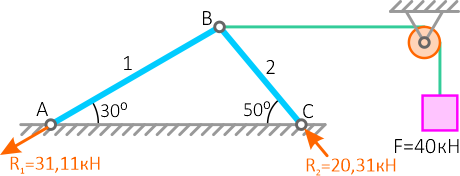
Ответ: R₁ = 31,11 кН и R₂ = 20,31 кН. Стержень №1 (AB) — растягивается, стержень №2 (BC) — сжимается.

Далее рассмотрены решения задач статики по соответствующим темам механики.

Порядок решения задач на равновесие системы сил
Решение практических заданий

Плоская система сил

1. Определение модуля и направления равнодействующей системы сходящихся сил
2. Составление уравнений суммы моментов сил относительно точки

Задачи на равновесие тела под действием произвольной плоской системы сил

1. Определение реакции шарнира и опоры
2. Определение реакций связей аналитическим и графическим способом
3. Определение реакций стержней треугольной системы, удерживающей два груза
4. Определение реакций опор балки, когда сила приложена под углом
5. Определение опорных реакций для разных способов нагружения

Задачи на равновесие составных конструкций под действием плоской системы сил

1. Реакции в шарнирах
2. Реакции опор и шарнира

Задачи на равновесие твердого тела при наличии трения

1. Вес груза для равновесия тела
2. Коэффициент трения обеспечивающий равновесие
3. Угол наклона плоскости при котором цилиндр начнет скатываться

Задачи на расчет пространственной системы сил

1. Вес противовеса и реакции шарниров
2. Величина груза для равновесия и реакции подшипников
3. Определение реакций подшипников пространственно нагруженного вала

Задачи на определение центра тяжести

Расчет координат центра тяжести:

1. пространственной фигуры
2. сложной несимметричной фигуры
3. тонкой однородной симметричной пластинки (плоской фигуры)
4. сложного сечения
5. объемного тела

Порядок решения задачи определения координат центра тяжести сложной фигуры в нашем коротком видео:

Другие видео

Другие расчеты равновесия системы сил

1. Определение усилий в стержнях
2. Натяжение троса и реакция опоры
3. Реакции опор в точках системы
4. Опорные реакции невесомой конструкции
5. Опорные реакции в скользящей заделке
6. Расчет реакций в бискользящей и глухой заделке
7. Реакции в скользящей заделке
8. Натяжение бесконечного ремня
9. Расчет усилия в стержне
10. Равновесие тела на шероховатой наклонной поверхности
11. Расчет силы для подъема тела по наклонной плоскости

---

Дополнительно: