Пример решения задачи по определению в заданный момент времени скорости, полного, касательного, нормального ускорений, радиуса кривизны и вида траектории точки по известным уравнениям её движения в координатной форме.
Задача
Даны уравнения движения точки M:
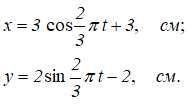
Требуется определить вид траектории и в момент времени t=1 c найти скорость точки, полное, касательное, нормальное ускорения и радиус кривизны траектории в данной точке.
Решение
Координатный способ задания движения – это траектория движения точки в параметрической форме.
Исключим из уравнений движения точки параметр t:
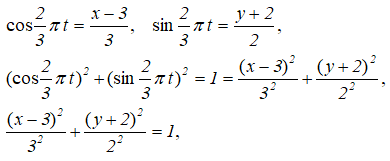
получили эллипс с полуосями 3 см и 2 см (рисунок 1.7).
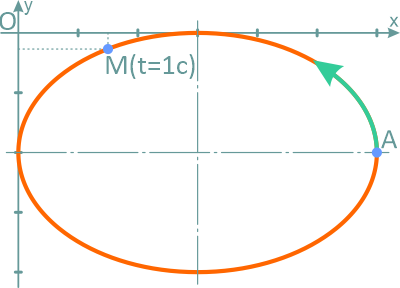
В момент времени t=1 c координаты точки:
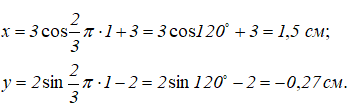
Движение начинается из точки A:
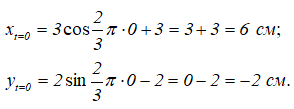
Учитывая графики изменения функций синуса и косинуса, можно утверждать, что точка M движется по эллипсу из точки A против хода часовой стрелки.
Скорость точки при координатном способе задания движения:
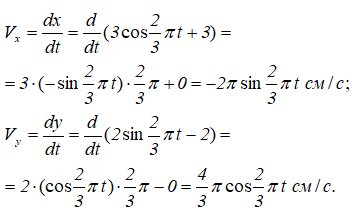
В момент времени t=1:
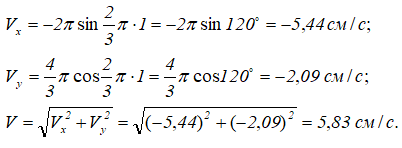
Направление вектора скорости определяется направляющими косинусами:
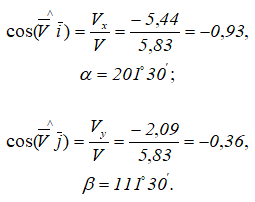
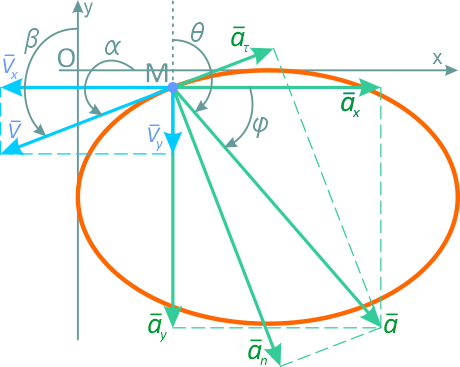
Таким образом, вектор скорости определен и по величине и по направлению (рисунок 1.8).
Ускорение точки при координатном способе задания движения:
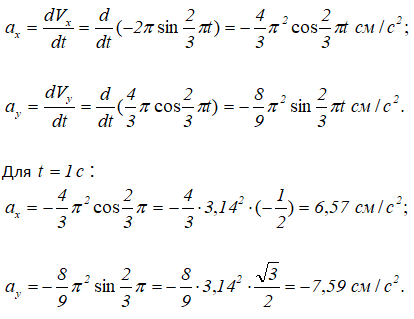
Полное ускорение:
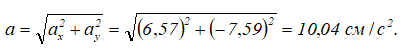
Направление вектора ускорения:
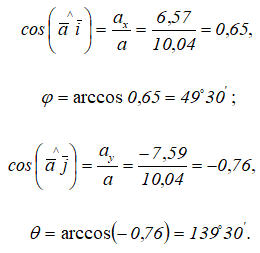
Результаты расчетов показаны на рисунке 1.8.
Касательное ускорение определяется по формуле (1.11):
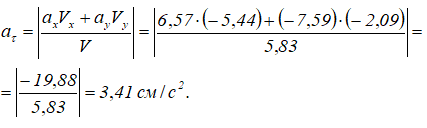
Нормальное ускорение можно определить либо из формулы (1.5), либо из формулы (1.12). По формуле (1.12) получим:
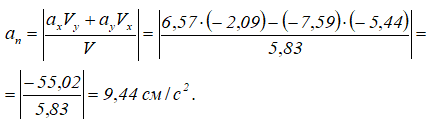
Результат расчета полного ускорения можно проверить:
![]()
Радиус кривизны траектории в точке M:
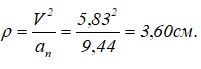
Результаты всех расчетов могут быть сведены в таблицу

Далее: