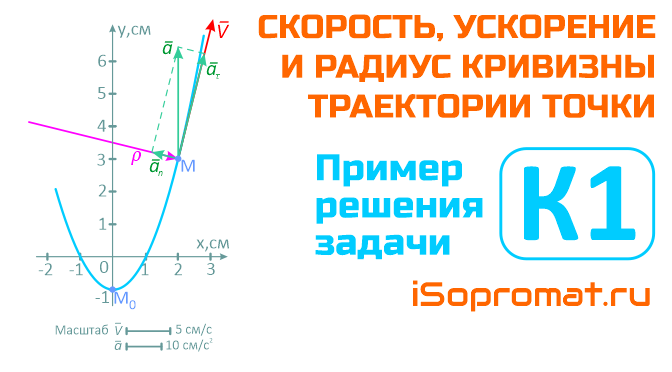
Решение задачи (РГР) К1 «Определение скорости и ускорения точки по заданным уравнениям ее движения» по разделу «кинематика» теоретической механики.
Пример определения для заданного момента времени положения точки на траектории, скорости, полного, касательного и нормального ускорения, радиуса кривизны траектории и вида траектории движения точки, если движение точки задано уравнениями.
Постановка задачи
Движение точки M задано уравнениями:
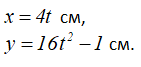
Требуется:
Установить вид траектории движения точки M, и для момента времени t = t1 = 0,5 с найти:
- положение точки на траектории,
- скорость, полное, касательное и нормальное ускорения,
- радиус кривизны траектории.
Решение РГР К1
Расчет траектории движения точки
Уравнения движения можно рассматривать как параметрические уравнения траектории точки.
Чтобы узнать вид траектории в координатной форме, надо получить прямую зависимость между переменными x и y, для этого избавимся от параметра времени t, выразив его, например, из первого уравнения и подставив во второе.
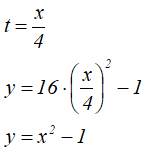
Получилось квадратное уравнение. То есть, точка движется по параболе.
Построим траекторию движения, рассчитав координаты нескольких её точек.
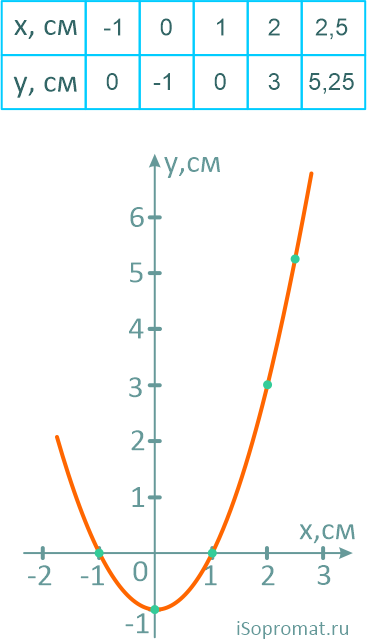
Определение положения точки на траектории
Определим положения точки в начале движения и в заданный момент времени.
Для этого в исходные уравнения подставляем соответственно сначала 0
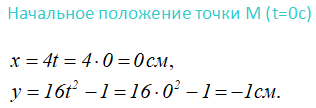
а затем, половину секунды.

Положение точки на ее траектории в заданный момент обозначим буквой M, и все остальные параметры будем рассчитывать для неё.
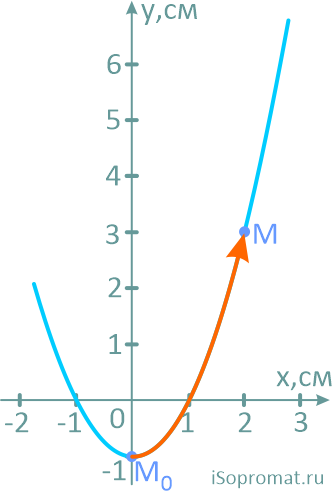
Расчет скорости точки
Направление и величину скорости точки определим как векторную сумму её проекций на оси координат.
![]()
Здесь i, j — орты осей x и y.
vx, vy — проекции вектора скорости на оси координат.
Проекции вектора скорости получим, взяв первые производные по времени t от соответствующих заданных уравнений движения точки.
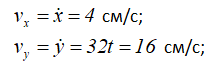
Далее выбрав масштаб, из точки M последовательно и с учетом знака, откладываем оба вектора.
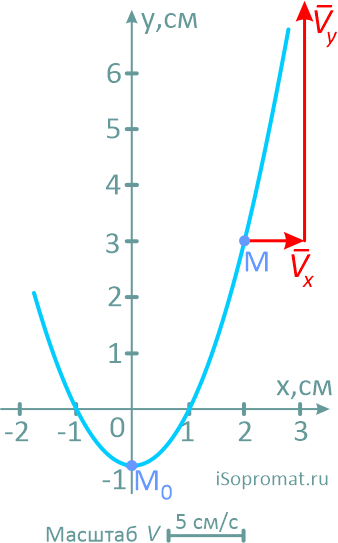
Сам вектор скорости получим, соединив точку M с концом второго вектора и направив его по ходу движения точки.
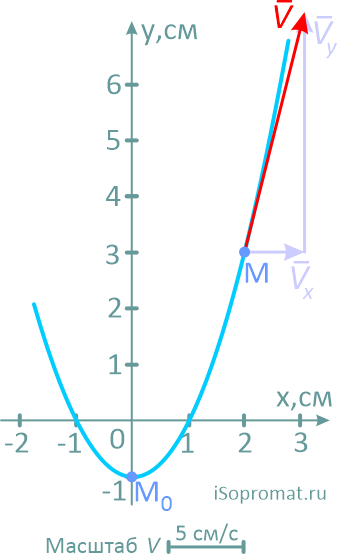
Здесь надо отметить, что вектор скорости всегда должен располагаться по касательной к траектории. Любое другое положение будет указывать на ошибки в расчетах.
Рассчитаем модуль вектора скорости
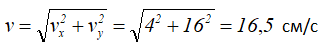
Расчет ускорений точки
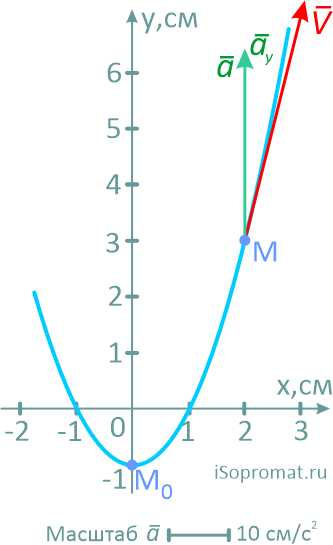
Проекции полного ускорения точки на оси координат определяются как вторая производная от исходных уравнений движения точки.

Здесь, ax, ay – проекции ускорения точки на оси координат.
В этом примере, горизонтальная проекция ускорения оказалась равной нулю, поэтому его модуль и направление будут совпадать с вертикальной.
![]()
Касательная составляющая полного ускорения это производная скорости точки по времени.
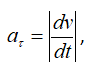
Ее можно рассчитать по этой формуле.
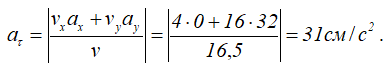
Вектор касательного ускорения всегда направлен по линии вектора скорости.
Положительная величина говорит об ускоренном движении точки и тогда направления скорости и касательного ускорения совпадают.
В противном случае они разнонаправлены, и движение точки замедляется.
Модуль нормального ускорения определим по формуле Пифагора, так как векторы касательного и центростремительного ускорений всегда взаимно перпендикулярны.
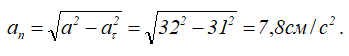
Расчет радиуса кривизны траектории
Осталось найти радиус кривизны траектории в точке M, который равен отношению квадрата скорости к модулю нормального ускорения.
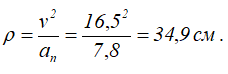
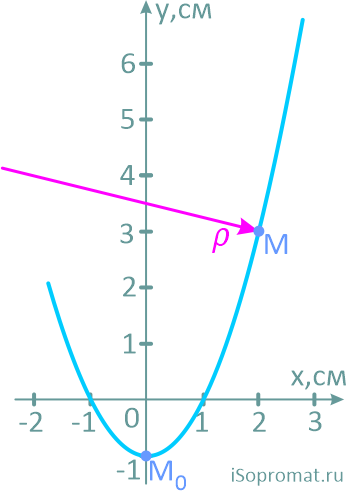
Результаты расчетов
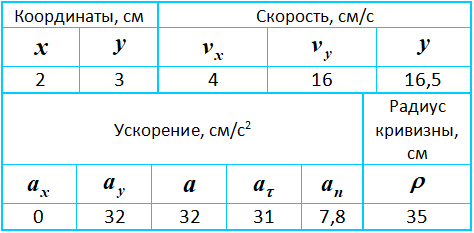
Результаты вычислений для заданного момента времени t1=0,5c приведены в таблице:
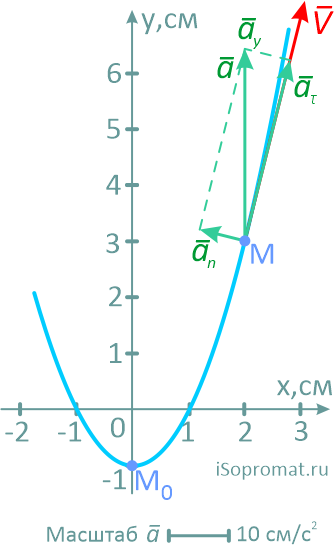
На рисунке показано положение точки M в заданный момент времени и векторы скорости и ускорений в выбранном масштабе.
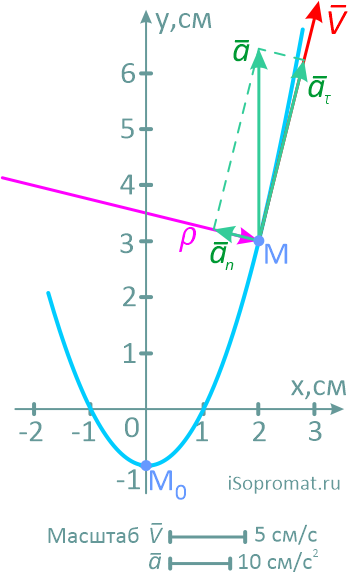
Вектор v строим по составляющим vx и vy, причем этот вектор должен по направлению совпадать с касательной к траектории.
Вектор a строим по составляющим ax и ay и затем раскладываем на составляющие векторы aτ и an.
Совпадение величин aτ и an, найденных из чертежа, с их значениями, полученными аналитически, служит критерием правильности решения.
Далее: