Пример решения задачи по определению координат положения центра тяжести трехмерной пространственно изогнутой стержневой (проволочной) фигуры.
Задача
Определить положение центра тяжести пространственно изогнутой проволочной фигуры (рисунок 2.5).
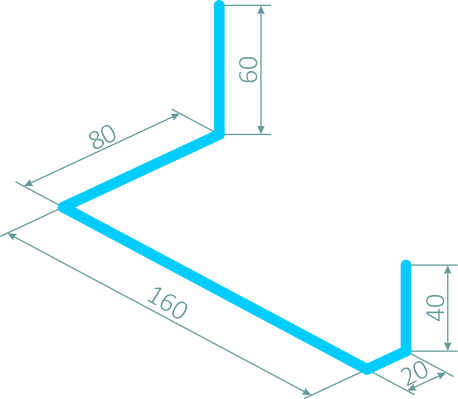
Размеры указаны в мм.
Другие примеры решений >
Помощь с решением задач >
Решение
Расположив стержневую фигуру в осях координат, разделим ее на пять прямолинейных участков 1, 2, 3, 4 и 5 и отметим точками C1, C2, C3, C4 и C5 центры тяжести каждого участка.
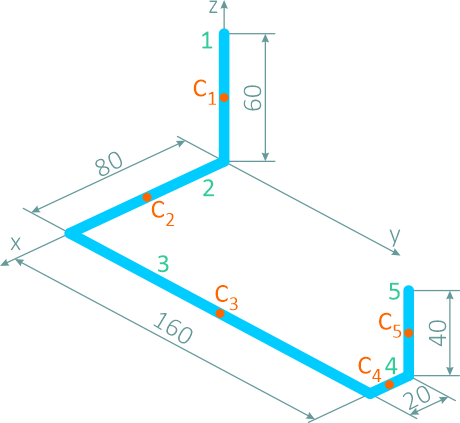
Исходные данные для определения координат центра тяжести фигуры (li – длины участков и координаты Ci в см):
l2 = 8 см, C2(4;0;0),
l3 = 16 см, C3(8;8;0),
l4 = 2 см, C4(7;16;0),
l5 = 4 см, C5(6;16;2).
Тогда, координаты центра тяжести трехмерной пространственной фигуры:
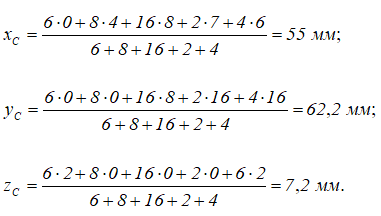
Таким образом, центр тяжести фигуры расположен в точке с координатами C (55,0; 62,2; 7,2)
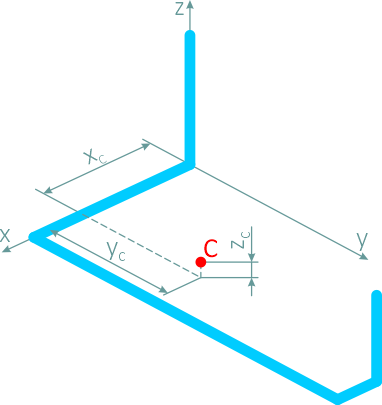
Положение центра тяжести пространственной фигуры определено!
Пример определения координат центра тяжести для сложных плоских фигур рассмотрен в нашем коротком видео:
Другие видео
