Пример решения задачи по определению координат положения центра тяжести тонкой однородной симметричной пластины методом отрицательных площадей.
Задача
Определить положение центра тяжести тонкой однородной пластинки, имеющей ось симметрии (рисунок 31).
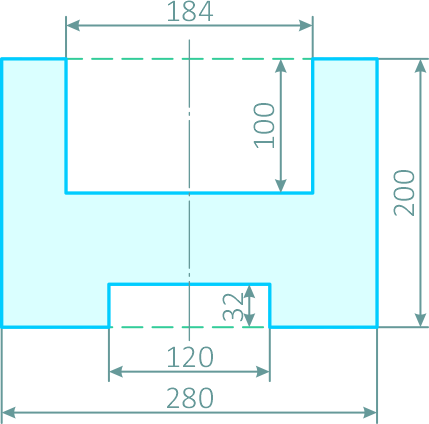
Рисунок 31
Решение
Пример определения координат центра тяжести для несимметричных фигур рассмотрен в нашем коротком видео:
Пластина симметрична, т.е. имеет ось симметрии, на которой находится центр тяжести. Совместим с осью симметрии ось y, а ось x – с нижним краем пластинки (абсцисса центра тяжести плоской фигуры xC = 0).
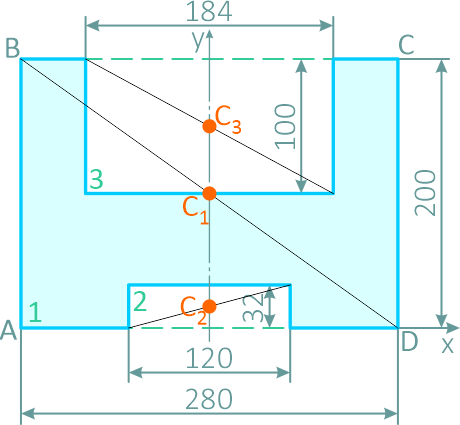
Рисунок 32
Дополнив пластинку до прямоугольника ABCD, разобьем ее на три части. Определим площади каждой части в см2 и координаты их центров тяжести в сантиметрах:
S1 = 28×20 = 560 см2; C1 (0;10);
S2 = 12×3,2 = 38,4 см2; C2 (0;1,6);
S3 = 18,4×10 = 184 см2; C3 (0;15).
Рассчитаем ординату центра тяжести плоской фигуры с помощью метода отрицательных площадей:
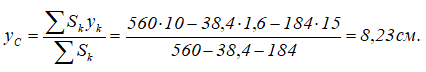
и отметим положение центра тяжести на самой фигуре
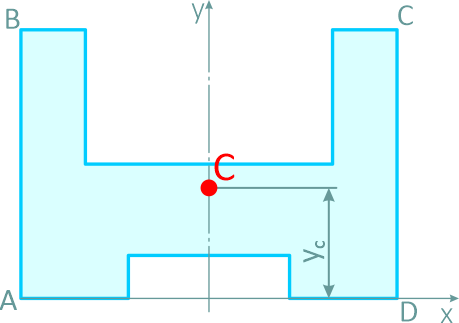
Рисунок 33
Далее: