Пример решения задачи по определению веса противовеса удерживающего в равновесии твердое тело и реакций шарниров, приоткрытой квадратной крышки, без учета сил трения на блоке.
Задача
Квадратная крышка весом 400 Н удерживается приоткрытой на угол α=60° над горизонтальной плоскостью противовесом Q (рисунок 20).
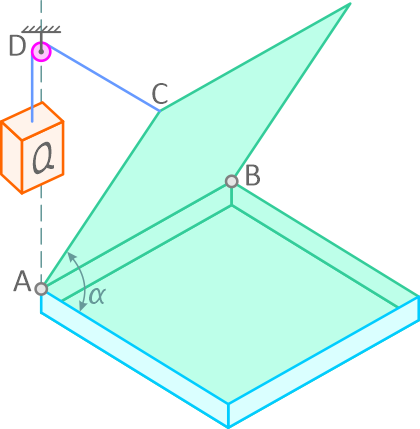
Определить, пренебрегая трением на блоке D, вес противовеса Q и реакции шарниров A и B, если блок D укреплен на одной вертикали с шарниром A и AD = AC.
Решение
Выбрав за начало координат точку A и расположив оси так, как показано на рисунке 21, покажем на этом же рисунке активные силы и реакции опор.
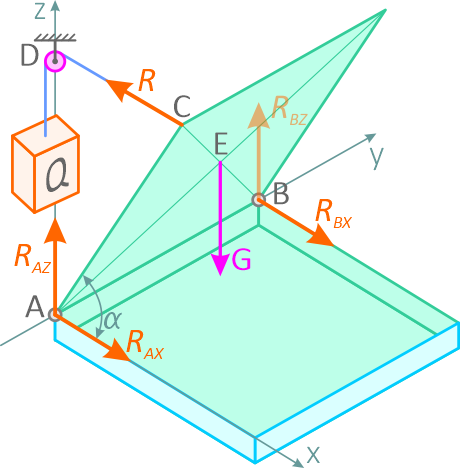
На крышку действует сила тяжести G, которую считаем приложенной в точке E (центр симметрии квадрата), и реакция R нити CD, приложенная в точке C.
Сила R численно равна весу Q противовеса. Действие этих сил уравновешивается реакциями шарниров A и B.
Так как силы R и G действуют в плоскостях, перпендикулярных к оси y, то реакции шарниров лежат в плоскостях, перпендикулярных к той же оси. Поэтому реакцию шарнира A заменим двумя составляющими RAx и RAy, а реакцию шарнира B – составляющими RBx и RBz.
Если составление уравнений равновесия по рисунку 21 затруднено, можно предварительно изобразить крышку вместе с действующими на нее силами в трех проекциях (рисунок 22):
- вид спереди (фронтальная проекция системы), ось x перпендикулярна к плоскости проекции;
- вид сверху (горизонтальная проекция), ось z перпендикулярна к плоскости проекции;
- вид слева (профильная проекция), ось y перпендикулярна к плоскости проекции.
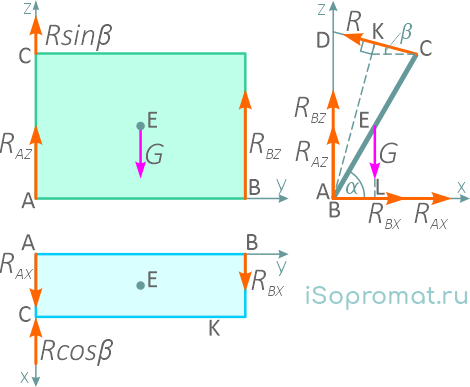
Составим уравнения равновесия (на ось y силы не проецируются, т.к. все они перпендикулярны этой оси):
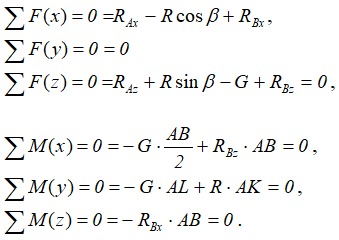
Решаем полученные уравнения:
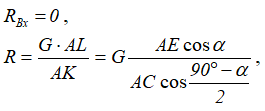
так как AE = AC/2, то
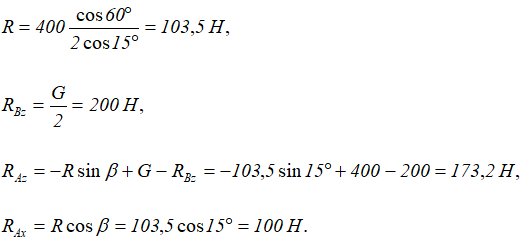
Полная реакция шарнира:
![]()
Таким образом, чтобы крышка находилась в равновесии приоткрытой под углом 60°, вес противовеса должен быть Q = R = 103,5 Н.
При этом реакция шарнира A имеет две составляющие: горизонтальную RAx = 100 Н и вертикальную RAz = 173,2 Н, а реакция шарнира B направлена вертикально и равна RB = 200 Н.
Далее: