Пример решения задачи по определению наименьшего угла α наклона плоскости, при котором цилиндр заданного радиуса начнет скатываться по плоскости без скольжения.

Задача

Определить наименьший угол α наклона плоскости к горизонту, при котором цилиндр радиуса r = 5 см начнет скатываться по плоскости, если коэффициент трения качения δ = 0,05 см.

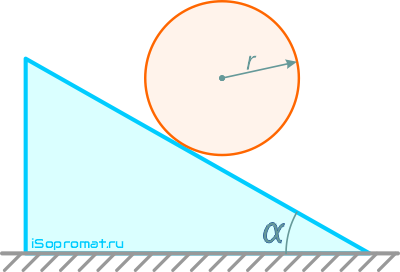
Проверить, возникает ли при этом сила трения скольжения, достаточная для осуществления качения цилиндра без скольжения, если коэффициент трения скольжения f = 0,08 (рисунок 27).

Решение

Рассматриваем критический (пусковой) момент равновесия цилиндра, когда момент сопротивления качению принимает максимальное значение: M_С^max=Nδ.

Отбрасывая связь, заменим ее действие на цилиндр силами реакции.

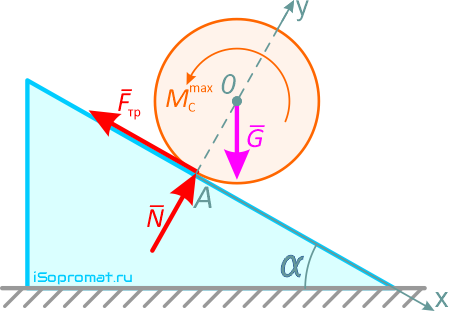
При этом на цилиндр, как на свободное твердое тело, будут действовать вес цилиндра G, нормальная реакция N наклонной плоскости, которая служит связью, сила трения скольжения F_тр, а также момент сопротивления качению M_С.

Составим уравнения равновесия произвольной плоской системы сил:

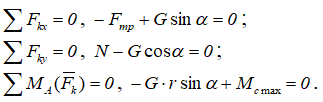
Учитывая, что M_С^max = Nδ, из второго уравнения получим

Тогда третье уравнение примет вид

откуда

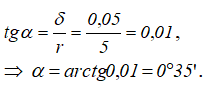
Из первого уравнения получаем выражение

в то время как максимальная сила трения скольжения

Отсюда видно, что условие F_тр ≤ F_тр^max соблюдается, а поэтому цилиндр начнет катиться по наклонной плоскости без скольжения.

---

Далее: