Пример расчета статически неопределимой балочно-стержневой системы (СНСС) на прочность и составление уравнения совместности деформаций для раскрытия статической неопределимости системы.
Задача
Абсолютно жесткий брус (балка), закрепленный в шарнирно неподвижной опоре и удерживаемый в горизонтальном положении двумя стержнями (тягами) 1 и 2, составляет статически неопределимую систему
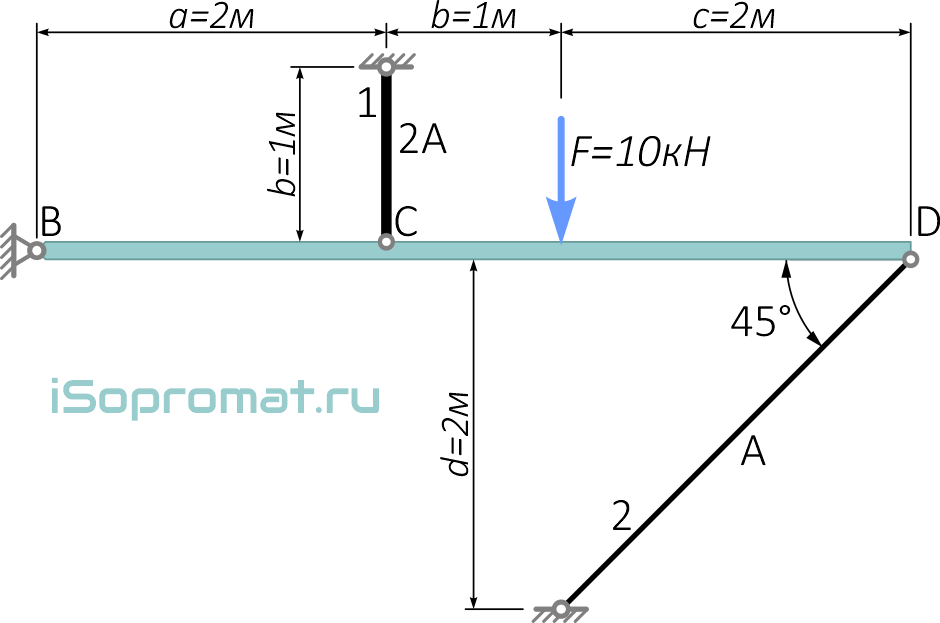
Один из стержней расположен под углом 45° к продольной оси бруса.
Площадь поперечного сечения стержня 1 должна быть в два раза больше площади сечения второго стержня A1=2A2.
Балка нагружена внешней поперечной сосредоточенной силой F=10кН.
Требуется:
- Раскрыть статическую неопределимость;
- Рассчитать внутренние усилия в стержнях системы;
- Определить по условию прочности диаметры стержней 1 и 2 при заданном соотношении площадей поперечного сечения.
Материал стержней – сталь, с пределом текучести σТ=240МПа, коэффициент запаса прочности nТ=1,5.
Решение
Заменим стержни внутренними продольными усилиями N.
Обозначим усилия в стержнях 1 и 2 соответственно N1 и N2.
Очевидно, что под действием силы F стержень 1 растягивается, стержень 2 – сжимается. Поэтому сразу зададим их реакциям соответствующие направления
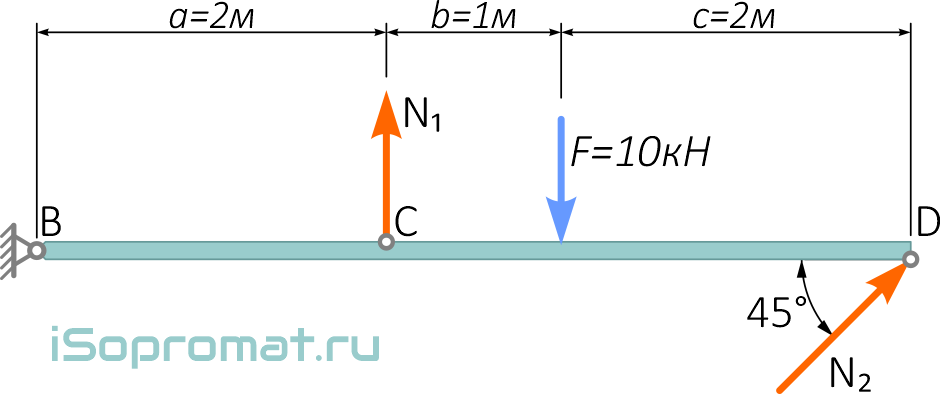
Раскрытие статической неопределимости стержневой системы
Определим степень статической неопределимости заданной системы.
В опорах системы возникает четыре неизвестных усилия – продольные силы в стержнях и две составляющие реакции в шарнирно неподвижной опоре B.
Для плоской системы можно составить только три уравнения равновесия.
![]()
т.е. система 1 раз статически неопределима.
Уравнение суммы моментов относительно точки B бруса
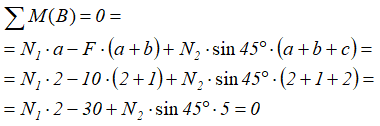
Для определения неизвестных усилий в стержнях, составленного уравнения равновесия недостаточно.
Следовательно, требуется составить дополнительное выражение — уравнение совместности деформаций стержней.
Для этого схематично покажем систему в деформированном состоянии, при котором брус BD под действием силы F повернулся относительно шарнира B на некоторый малый угол
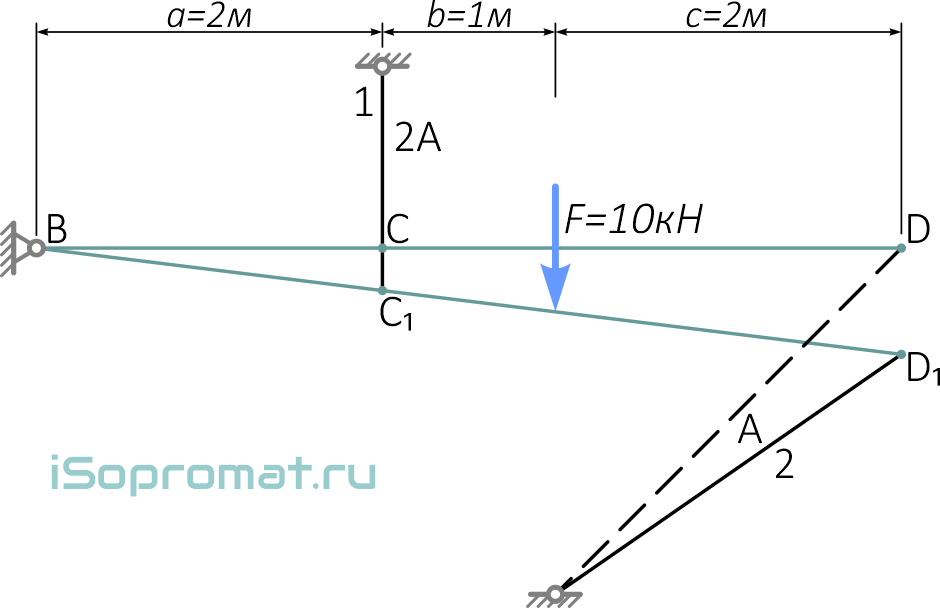
Для малых углов поворота бруса, перемещения его точек можно считать вертикальными.
В результате деформации системы, точка C стержня №1 перемещается в положение C1, а точка D стержня №2 в положение D1
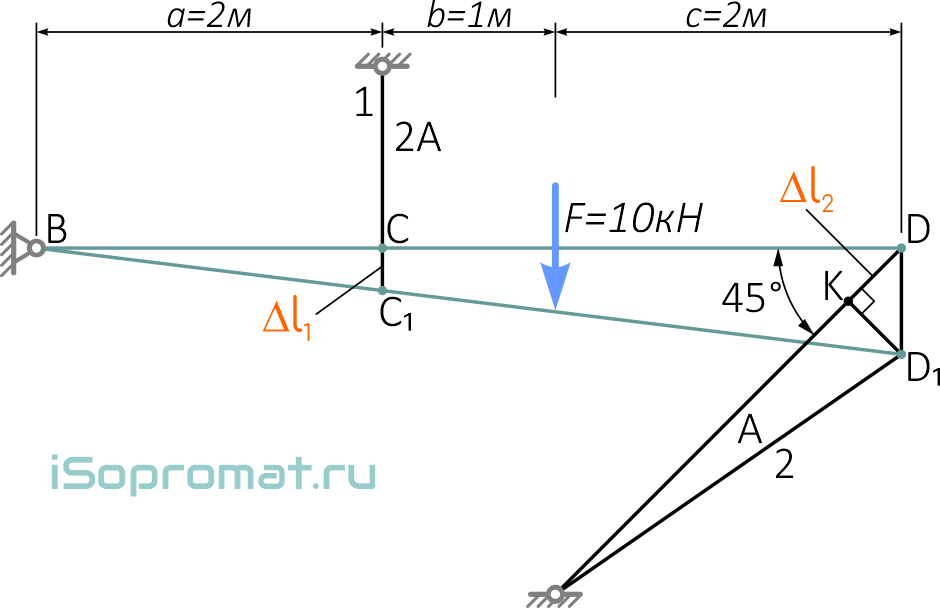
При этом изменится длина стержней: стержень 1 растянется на величину Δl1 (отрезок CC1), стержень 2 сожмется на Δl2 (DK).
Для определения изменения длины стержней расположенных под углом, из крайней точки D1 стержня проводится линия D1K, перпендикулярная начальному положению стержня.
Деформации стержней при растяжении и сжатии (по закону Гука):
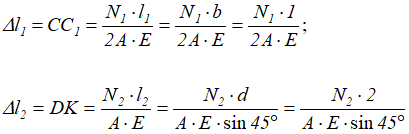
Определив геометрическую зависимость между этими деформациями, получим второе уравнение для расчета усилий в стержнях.
Из подобия треугольников BCC1 и BDD1 находим взаимную зависимость перемещений точек C и D
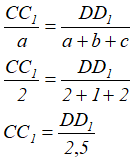
Откуда получаем зависимость (совместность) деформаций стержней 1 и 2
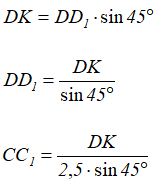
и зависимость между усилиями N1 и N2
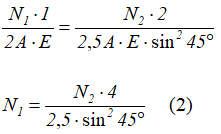
Подставляем полученное выражение в уравнение равновесия (1) и находим величину N2
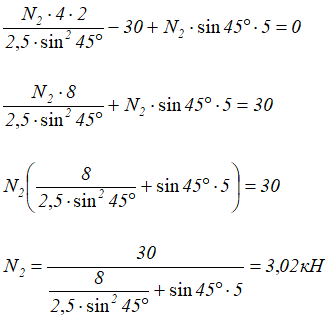
Статическая неопределимость стержневой системы раскрыта.
Из уравнения (2) рассчитываем величину усилия N1
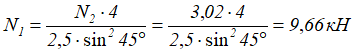
Расчет стержневой СНС на прочность
Допускаемое напряжение для материала стержней
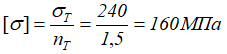
Из условия прочности определяем расчетные площади сечения A1 и A2 и диаметры d1 и d2 стержней
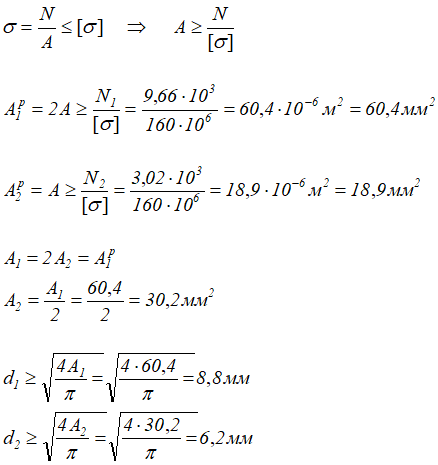
Проверка на прочность
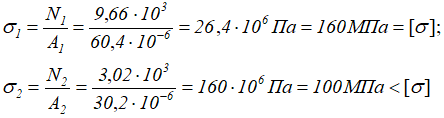
Прочность статически неопределимой стержневой системы обеспечена.
Ответ: площади сечения стержней: d1=8,8мм, d2=6,2мм.
Далее: