Пример раскрытия статической неопределимости с последующей проверкой на прочность стального стержня при растяжении и сжатии, закрепленного между жесткими заделками и нагруженного продольными сосредоточенными силами.
Задача
Статически неопределимый стальной прямой ступенчатый стержень, левым и правым торцами жестко закреплен между двумя опорами типа заделка.
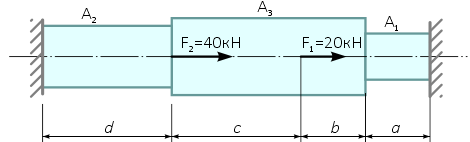
К стержню приложены две внешние продольные силы F1 и F2. Продольные размеры и площади сечений стержня заданы.
По условию задачи требуется:
- Раскрыть статическую неопределимость стержня;
- Определить реакции опор в заделках;
- Построить эпюру внутренних продольных сил N;
- Построить эпюру нормальных напряжений;
- Проверить прочность стержня если допустимые нормальные напряжения равны [σ] = 120МПа.
Дано (Вариант 3):
Величина внешних продольных сил F1 = 20кН и F2 = 40кН.
Продольные размеры участков бруса a = 0,5м, b = 0,5м, c = 1м, d = 1м.
Площади поперечных сечений стержня A1 = 9см2, A2 = 16см2, A3 = 25см2.
Пример решения
Вычерчиваем заданную расчетную схему бруса в масштабе, указываем числовые значения приложенных нагрузок и продольных размеров.
Раскрытие статической неопределимости стержня
Раскроем статическую неопределимость стержня и определим опорные реакции в заделках.
Для этого направим реакции опор произвольно, например, влево, так как заданные внешние силы направлены вправо.
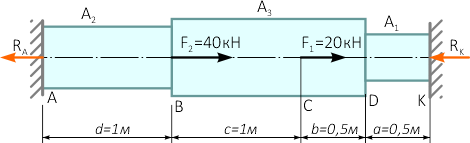
Для определения двух неизвестных требуется два уравнения.
Но для линейной системы сил можно составить только одно уравнение равенства нулю суммы проекций всех усилий на продольную ось z.
Следовательно, степень статической неопределимости стержня равна 1.
Уравнение равновесия стержня
![]()
Второе уравнение получим, рассмотрев зависимость деформаций участков стержня (уравнение совместности деформаций).
Расстояние между заделанными торцами стержня в результате действия на стержень всех сил, а, следовательно, его общая длина не изменится.
Получаем уравнение совместности деформаций в его общем виде:
![]()
Зная формулу расчета изменения длины участков стержня
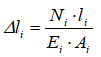
получаем уравнение совместности деформаций для заданного статически неопределимого стержня
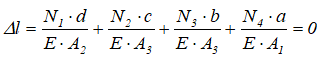
Так как материал на всех участках стержня одинаков, то E = const, и можно сократить выражение на модуль Юнга.
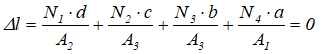
Выразим внутренние силы N через внешние силы и реакцию опоры, например левой части стержня
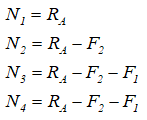
Записываем уравнение совместности деформаций через внешние усилия
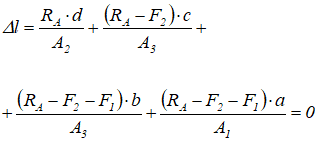
и подставляем в уравнение соответствующие значения сил, продольных размеров и площадей поперечного сечения.
Примечание: Если по условию задачи площади поперечных сечений заданы не явно, а в виде их соотношений (например, A, k1A и k2A) то в уравнения совместности деформаций подставляются их коэффициенты (соответственно 1, k1 и k2).
Откуда находим величину реакции RA
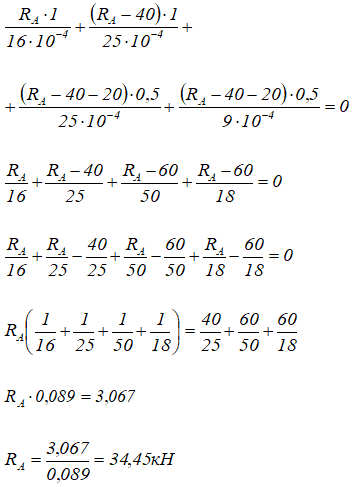
Статическая неопределимость стержня раскрыта.
Подставив полученное значение в уравнение равновесия, находим вторую реакцию заделке RK
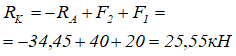
Положительные значения реакций означают, что изначально заданные направления оказались верными.
Реакция RA растягивает стержень, RK — сжимает.
Построение эпюры продольных сил N
Рассчитаем величину внутренних продольных сил N по участкам
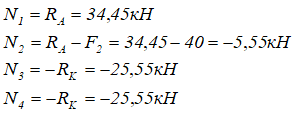
По полученным данным строим эпюру внутренних продольных сил N.
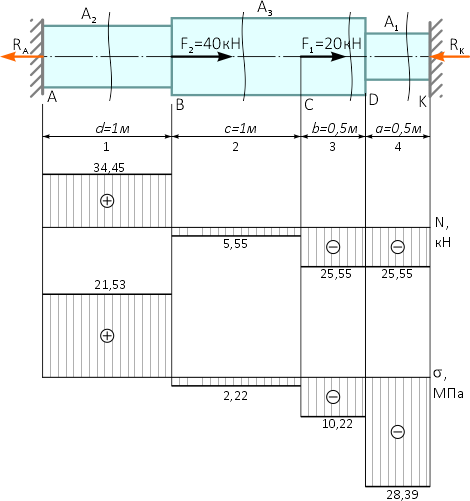
На эпюре скачки значений внутренней продольной силы в сечениях стержня, где приложены внешние силы, включая реакции в опорах.
Эти скачки равны величине этих сил. Эпюра построена правильно.
Расчет нормальных напряжений и проверка стержня на прочность
Расчет значений нормальных напряжений в поперечных сечениях стержня по участкам
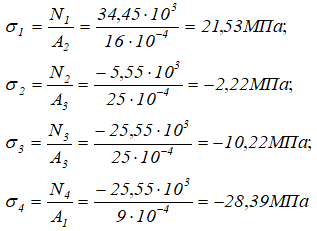
По полученным данным строим эпюру нормальных напряжений σ
По эпюре видно, что наибольшее по модулю напряжение имеет место на четвертом участке (DK) стержня, и равно σmax = 28,39 МПа.
Максимальное нормальное напряжение меньше допустимого значения, следовательно, стержень прочный.
Статическая неопределимость раскрыта, прочность стержня проверена.
Далее: