Условие прочности при растяжении и сжатии: нормальные напряжения σ в сечениях бруса не должны превышать допустимых напряжений [σ] для заданного материала.
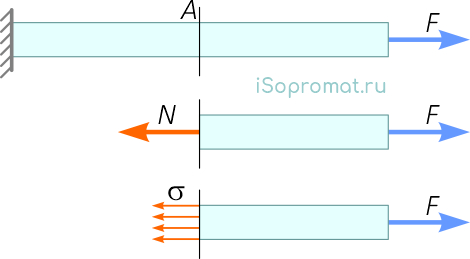
При продольном осевом нагружении (растяжении-сжатии) в поперечных сечениях бруса имеют место только нормальные напряжения σ. Поэтому для обеспечения прочности стержней и стержневых систем необходимо и достаточно выполнение условия:
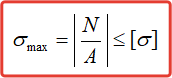
Здесь
σmax – максимальные расчетные нормальные напряжения в стержне,
N – значения внутренних продольных сил в соответствующих сечениях (принимаются с построенных эпюр),
А – площадь поперечного сечения бруса на рассматриваемом участке,
[σ] – допустимые напряжения (расчетное сопротивление) для материала стержня, определяемое по формуле:
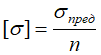
где n – коэффициент запаса прочности, устанавливаемый нормативными документами.
σпред — предельные напряжения для материала стержня
Для пластичных материалов (δ > 5%)
![]()
σТ — предел текучести.
Для хрупких материалов (δ ≤ 5%)
![]()
σВ — временное сопротивление.
В случаях, когда для материала стержней допустимые напряжения на растяжение [σ]р и на сжатие [σ]сж отличаются, при сравнении необходимо учитывать знак напряжений.
Так, положительные (растягивающие) значения напряжений сравниваются с [σ]р, отрицательные (сжимающие) напряжения по модулю не должны превышать значения [σ]сж.
Три задачи сопромата
Условие прочности позволяет решать три основных типа задач сопротивления материалов и технической механики:
- Проверка на прочность
- Подбор размеров сечения (проектировочный расчет)
- Определение грузоподъемности
Проверка на прочность
В случае, когда известны внешние нагрузки, а также размеры и материал стержня можно выполнить проверку его прочности. Для этого по каждому участку рассчитывается величина нормальных напряжений σ, после чего, максимальная из них сравнивается с допустимым значением [σ].
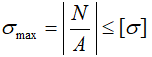
Ответ в задаче данного типа дается в виде заключения:
- если σmax ≤ [σ] — стержень прочный,
- если σmax > [σ] — стержень непрочный.
Подбор размеров сечения (проектировочный расчет)
Эта задача является основной в сопромате и технической механике. Здесь, по известным схеме нагружения и материалу стержня определяется минимально необходимая площадь поперечного сечения A обеспечивающая его прочность.
Для этого условие прочности записывается относительно искомой величины.
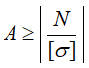
Полученные размеры в случае необходимости можно только увеличивать. Уменьшение размеров приведет к превышению напряжениями допустимых значений.
Определение грузоподъемности стержня
Формула позволяет по известным размерам и материалу рассчитать величину допустимой внутренней продольной силы, которую может выдержать стержень, оставаясь прочным.
![]()
В данном случае условие прочности записано относительно внутренней силы N.
Далее: